题目内容
对数的性质与运算法则(以下标中a>0且a≠1,m、n>0,b>0且b≠1)
(1)①loga1=______②logaa=______③负数与零没有对数
(2)①logaMN=______. ②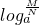 =______. ③
=______. ③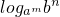 =______.
=______.
(3)①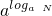 =______. ②lg2+lg5=______.
=______. ②lg2+lg5=______.
解:(1)①令loga1=x,则化为指数式即ax=1,∴x=0,即 loga1=0.
②令logaa=y,化为指数式ay=a∴y=1,logaa=1
③因为指数函数大于0,所以,负数与零没有对数.
(2) ①设am=M,an=N,am•an=am+n=M•N,由对数的定义,
logaM=m,logaN=n,得:m+n=logaMN,∴logaMN=logaM+logaN.
②∵ =am-n,设am=M,an=N,则am-n=
=am-n,设am=M,an=N,则am-n=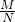 ,由对数的定义,
,由对数的定义,
logaM=m,logaN=n,m-n= ,∴
,∴ =logaM-logaN.
=logaM-logaN.
③由①得: =logam+
=logam+ =logam+nlogab,
=logam+nlogab,
∴ =logam+nlogab,
=logam+nlogab,
(3) ①令 =t,化为对数式得:logaN=logat,∴N=t,即
=t,化为对数式得:logaN=logat,∴N=t,即 =N
=N
②lg2+lg5=lg10=1.
分析:利用对数函数的运算法则进行求值.
点评:本题考查对数函数的运算法则.
②令logaa=y,化为指数式ay=a∴y=1,logaa=1
③因为指数函数大于0,所以,负数与零没有对数.
(2) ①设am=M,an=N,am•an=am+n=M•N,由对数的定义,
logaM=m,logaN=n,得:m+n=logaMN,∴logaMN=logaM+logaN.
②∵
 =am-n,设am=M,an=N,则am-n=
=am-n,设am=M,an=N,则am-n=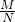 ,由对数的定义,
,由对数的定义,logaM=m,logaN=n,m-n=
 ,∴
,∴ =logaM-logaN.
=logaM-logaN.③由①得:
 =logam+
=logam+ =logam+nlogab,
=logam+nlogab,∴
 =logam+nlogab,
=logam+nlogab,(3) ①令
 =t,化为对数式得:logaN=logat,∴N=t,即
=t,化为对数式得:logaN=logat,∴N=t,即 =N
=N②lg2+lg5=lg10=1.
分析:利用对数函数的运算法则进行求值.
点评:本题考查对数函数的运算法则.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
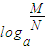 = . ③
= . ③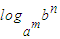 = .
= .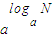 = . ②lg2+lg5= .
= . ②lg2+lg5= .