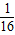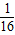题目内容
一动圆圆心在抛物线x2=-8y上，且动圆恒与直线y-2=0相切，则动圆必过定点（ ）
| A．（4，0） | B．（0，-2） | C．（2，0） | D．（0，-4） |
∵动圆圆心在抛物线x2=-8y上，且动圆恒与直线y-2=0相切，而抛物线的焦点为（0，-2），准线是y-2=0，
故动圆圆心到焦点的距离等于它到准线的距离，故动圆必过抛物线的焦点（0，-2），
故选B．
故动圆圆心到焦点的距离等于它到准线的距离，故动圆必过抛物线的焦点（0，-2），
故选B．
练习册系列答案
相关题目
一动圆圆心在抛物线x2=4y上，过点（0，1）且与定直线l相切，则l的方程为（ ）
| A、x=1 | ||
B、x=
| ||
| C、y=-1 | ||
D、y=-
|
C.y=-1 D.y=-
