题目内容
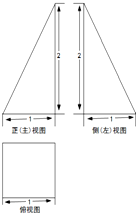（2012•天河区三模）一个几何体的三视图如图所示，则这个几何体的表面积为3+
| 5 |
3+
．| 5 |
分析：利用三视图判断该几何体的结构，然后求出对应的表面积．
解答：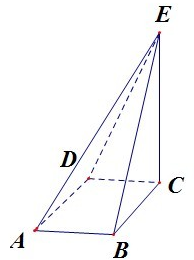
解：由三视图可知该几何体是个四棱锥．
底面四边形为边长为1的正方形，一条侧棱和底面垂直，如图PC⊥面ABCD．
且EC=2．
所以EB=ED=
，
所以侧面积为2(
×1×2+
×1×
)=2(1+
)=2+
，底面积为1．
所以该几何体的表面积为2+
+1=3+
．
故答案为：3+
．
解：由三视图可知该几何体是个四棱锥．底面四边形为边长为1的正方形，一条侧棱和底面垂直，如图PC⊥面ABCD．
且EC=2．
所以EB=ED=
| 5 |
所以侧面积为2(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5 |
所以该几何体的表面积为2+
| 5 |
| 5 |
故答案为：3+
| 5 |
点评：本题考查三视图求几何体的体积，考查计算能力，空间想象能力，三视图复原几何体是解题的关键．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
（2012•天河区三模）函数y=f（x）（x∈R）的图象如图所示，下列说法正确的是（ ）