Question

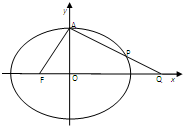设椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的左焦点为F，上顶点为A，过点A作垂直于AF的直线交椭圆C于另外一点P，交x轴正半轴于点Q，且

AP

=

8

5

PQ

．
（1）求椭圆C的离心率；
（2）若过A、Q、F三点的圆恰好与直线l：x+

3

y-5=0相切，求椭圆C的方程．

Answer 1

分析：（1）设出Q点坐标，由F，A的坐标表示出

FA

和

AQ

，根据

FA

⊥

AQ

，得出

FA

•

AQ

=0，进而求得x₀，设P（x₁，y₁）根据

AP

=

8

5

PQ

，求得x₁和y₁的表达式，把点P的坐标代入椭圆方程进而求得a和c的关系，则椭圆的离心率可得．
（2）根据（1）中a和c的关系可知F和Q的坐标，△AQF的外接圆圆心和半径，进而根据

| 1 2 a-5|

2

=a，求得a，进而根据a和b，c的关系求得b，则椭圆的方程可得．

解答：解：（1）设Q（x₀，0），
由F（-c，0），A（0，b）知

FA

=（c，b），

AQ

=（x₀，-b），
∵

FA

⊥

AQ

，
∴

FA

•

AQ

=0，
即cx0-b2=0，解得x0=

b2

c

，
设P（x₁，y₁），由于

AP

=

8

5

PQ

，
得x₁=

8b2

13c

，y₁=

5b

13

，
∵点P在椭圆上，
∴

( 8b2 13c )2

a2

+

( 5b 13 )2

b2

=1，整理得2b²=3ac，即2（a²-c²）=3ac，
则2e²+3e-2=0，解得e=

1

2

，
故椭圆的离心率e=

1

2

．
（2）由（1）知2b²=3ac，得到

b2

c

=

3

2

a，
又由

c

a

=

1

2

，得到c=

1

2

a，
于是F（-

1

2

a，0）Q（

3

2

a，0），
△AQF的外接圆圆心为（

1

2

a，0），半径r=

1

2

|FQ|=a，
则

| 1 2 a-5|

2

=a，解得a=2，∴c=1，b=

3

，
故所求椭圆方程为

x2

4

+

y2

3

=1．

点评：本题主要考查了直线与圆锥曲线的综合问题．解题的前提的是熟练掌握椭圆的基本性质．