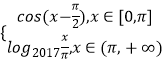Question

【题目】已知函数，

（1）若的解集为，求的值；

（2）求函数在上的最小值；

（3）对于，使成立，求实数的取值范围．

Answer 1

【答案】(1) .

(2).

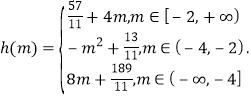(3).

【解析】

第一问将题的条件转化，得到一个关于的一元二次不等式，利用不等式解的特征，可知边界值为其对应的方程的根，应用根与系数之间的关系，确定出系数的值，第二问通过对对称轴位置的讨论，确定出函数在哪个点处取得最小值，第三问将问题转化为在相应区间上，从而求得结果.

（1）由得；整理得，

因为不等式的解集为，

所以方程的两根是，；

由根与系数的关系得 ，即；

（2）的对称轴方程为，

①当时，即 在上是单调增函数，故；

②当时，即，在上是单调减函数，在上是单调增函数，故；

③当时，即 在上是单调减函数，故；

所以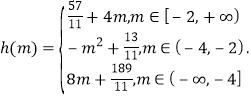

（3）因为函数在区间上为增函数，在区间上为减函数

其中，，所以函数在上的最小值为

对于使成立在上的

最小值不大于在上的最小值，

由（2）知

①

解得,所以；

②当时,

解得，所以；

③当时，

解得，所以

综上所述，的取值范围是.