题目内容
17.若函数f(x+1)的定义域为[-$\frac{1}{2}$,2],求函数f(x-1)的定义域.分析 由已知中函数f(x+1)的定义域为[-$\frac{1}{2}$,2],可以求出函数f(x)的定义域,进而求出函数f(x-1)的定义域.
解答 解:∵函数f(x+1)的定义域为[-$\frac{1}{2}$,2],即$-\frac{1}{2}$≤x≤2,
则$\frac{1}{2}$≤x+1≤3,
若$\frac{1}{2}$≤x-1≤3,
则$\frac{3}{2}$≤x≤4.
故函数f(x-1)的定义域为[$\frac{3}{2}$,4],
故答案为:[$\frac{3}{2}$,4].
点评 本题考查的知识点是函数的定义域及其求法,其中熟练掌握抽象函数定义域求解时“一不变(括号里整体的取值范围不变),应万变”的原则是解答此类问题的关键.

练习册系列答案
相关题目
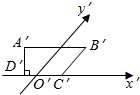 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积. 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.