题目内容
如图,直角梯形OABC中AB//OC,AB=1,OC=BC=2,直线 截该梯形所得位于
截该梯形所得位于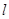 左边图形面积为
左边图形面积为 ,则函数
,则函数 的图像大致为( )
的图像大致为( )
C
解析试题分析:本题考查的是函数的图象和分段函数的综合类问题.在解答的过程当中,首先应该直线l的运动位置分析面积的表达形式,当 ,则阴影部分是三角形面积,直线OA的方程:y=2x,则根据三角形的面积公式得到
,则阴影部分是三角形面积,直线OA的方程:y=2x,则根据三角形的面积公式得到 ,
,
当 ,则阴影部分的面积为梯形面积减去了矩形的面积即可,则可知
,则阴影部分的面积为梯形面积减去了矩形的面积即可,则可知 ,进而得到分段函数:
,进而得到分段函数:
结合不同段上函数的性质,可知第一段是二次曲线,第二段是直线,排除法可知选项C符合.故选C.
考点:本题考查的是函数的图象和分段函数的综合类问题。通过求解函数的解析式来表示图形的面积,进而分析面积的变化情况。是中档题。
点评:在解答的过程当中充分体现了分段函数的知识、分类讨论的思想以及函数图象的知识.值得同学们体会和反思。

练习册系列答案
相关题目
已知定义在R上的奇函数 和偶函数
和偶函数 满足
满足
 ,若
,若 ,则
,则
A. | B. | C. | D.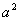 |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B.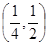 | C.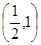 | D.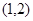 |
下列四组函数中表示同一函数的是( )
A. , , |
B. |
C. , , |
D. , ,  |
若函数 在
在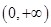 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 为
为 上的减函数,则满足
上的减函数,则满足 的实数
的实数 的取值范围是( )
的取值范围是( )
A. | B.(0,1) | C. | D. |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A. | B. | C. | D. |
 ,函数
,函数 与
与 的图像可能是( )
的图像可能是( )
 的图象如图1所示 , 则其导函数
的图象如图1所示 , 则其导函数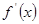 的图象大致形状是( )
的图象大致形状是( ) 