题目内容

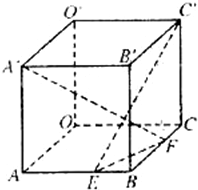
在棱长为a的正方体OABC—O1A1B1C1中,E、F分别是AB、BC上的动点,且AE=BF.求证:A1F⊥C1E.

证明:以O为坐标原点建立如图所示的空间直角坐标系,则A1(a,0,a),C1(0,a,a).

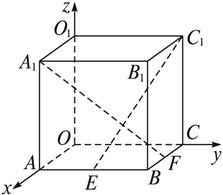
设AE=BF=x,∴E(a,x,0),F(a-x,a,0).

∴=(-x,a,-a),=(a,x-a,-a).

∵·=(-x,a,-a)·(a,x-a,-a)

=-ax+ax-a2+a2

=0,

∴⊥,即A1F⊥C1E.

练习册系列答案
相关题目
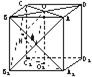精英家教网（甲）如图，已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC，∠ABC=90°，BC=2，AC=2
3
，又AA1⊥A1C，AA1=A1C．
（1）求侧棱A1A与底面ABC所成的角的大小；
（2）求侧面A1B与底面所成二面角的大小；
（3）求点C到侧面A1B的距离．
（乙）在棱长为a的正方体OABC-O'A'B'C'中，E，F分别是棱AB，BC上的动点，且AE=BF．
（1）求证：A'F⊥C'E；
（2）当三棱锥B'-BEF的体积取得最大值时，求二面角B'-EF-B的大小（结果用反三角函数表示）．
精英家教网如图，在棱长为a的正方体ABCD-A1B1C1D1中，M、O、O1分别是A1B、AC、A1C1的中点，且OH⊥O1B，垂足为H．
（1）求证：MO∥平面BB1C1C；
（2）分别求MO与OH的长；
（3）MO与OH是否为异面直线A1B与AC的公垂线？为什么？求这两条异面直线间的距离．
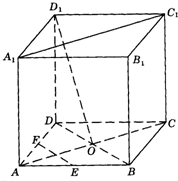精英家教网如图，在棱长为a的正方体ABCD-A1B1C1D1中，O是AC、BD的交点，E，F分别是AB与AD的中点．
（1）求证：直线OD1与直线A1C1垂直；
（2）求异面直线EF与A1C1所成角的大小；
（3）求二面角B-AC-D1的大小．
（2001•上海）在棱长为a的正方体OABC-O′A′B′C′中，E、F分别是棱AB、BC上的动点，且AE=BF．
（Ⅰ）求证：A′F⊥C′E；
（Ⅱ）当三棱锥B′-BEF的体积取得最大值时，求二面角B′-EF-B的大小．（结果用反三角函数表示）
在棱长为a的正方体OABC-O′A′B′C′中，E、F分别是棱AB、BC上的动点，且AE=BF．
（Ⅰ）求证：A′F⊥C′E；
（Ⅱ）当三棱锥B′-BEF的体积取得最大值时，求二面角B′-EF-B的大小．（结果用反三角函数表示）
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网