题目内容
已知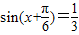 ,则sin2x的值为 .
,则sin2x的值为 .
【答案】分析:利用两角和的正弦函数展开表达式,通过平方即可求解sin2x与cos2x的关系式,然后求解sin(2x-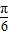 )与cos(2x-
)与cos(2x-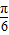 )的值.通过角的变换求解sin2x.
)的值.通过角的变换求解sin2x.
解答:解:因为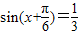 ,
,
所以sinxcos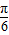 +cos
+cos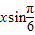 =
= ,
,
即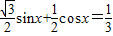 ,
,
两边平方可得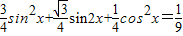 ,
,
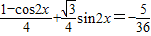 ,
,
所以sin(2x-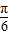 )=-
)=- ,cos(2x-
,cos(2x-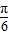 )=
)=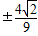 .
.
所以sin2x=sin(2x-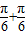 )=sin(2x-
)=sin(2x-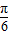 )cos
)cos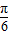 +sin
+sin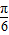 cos(2x-
cos(2x-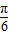 )=
)=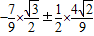 =
=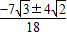 .
.
故答案为: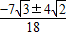
点评:本题考查两角和的正弦函数的应用,角的变换的技巧,同角三角函数的基本关系式的应用,考查计算能力.
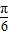 )与cos(2x-
)与cos(2x-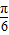 )的值.通过角的变换求解sin2x.
)的值.通过角的变换求解sin2x.解答:解:因为
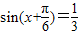 ,
,所以sinxcos
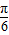 +cos
+cos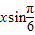 =
= ,
,即
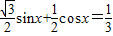 ,
,两边平方可得
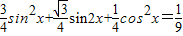 ,
,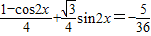 ,
,所以sin(2x-
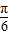 )=-
)=- ,cos(2x-
,cos(2x-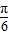 )=
)=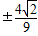 .
.所以sin2x=sin(2x-
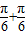 )=sin(2x-
)=sin(2x-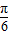 )cos
)cos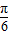 +sin
+sin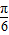 cos(2x-
cos(2x-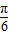 )=
)=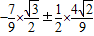 =
=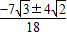 .
.故答案为:
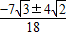
点评:本题考查两角和的正弦函数的应用,角的变换的技巧,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 ,则sin2x的值是( )
,则sin2x的值是( )



 ,则sin2x的值为( )
,则sin2x的值为( )



 ,则sin2x的值是( )
,则sin2x的值是( )



 ,则sin2x的值为( )
,则sin2x的值为( )



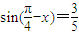 ,则sin2x的值为( )
,则sin2x的值为( )


