题目内容
请考生从以下三个小题中任选一个作答,若多选,则按所选的第一题计分.
A.(不等式选讲)若实数 满足
满足 ,则
,则 的最大值为_________.
的最大值为_________.
B.(几何证明选讲)以 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且 与圆
与圆 相切.若
相切.若 ,则
,则 _________.
_________.
C.(坐标系与参数方程)在极坐标系中,曲线 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________.
【答案】
A. B.
B. C.
C.
【解析】
试题分析:A:根据题意,由于实数 满足
满足 ,故可知有
,故可知有 故可知
故可知 =3(a+b+c)+b+2c,根据均值不等式来求解得到最大值为
=3(a+b+c)+b+2c,根据均值不等式来求解得到最大值为
B、根据题意,由于以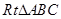 的直角边
的直角边 为直径的圆
为直径的圆 交
交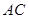 边于点
边于点 ,点
,点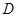 在
在 上,且
上,且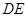 与圆
与圆 相切.根据弦切角定理,以及直径所对的圆周角为直角,那么若
相切.根据弦切角定理,以及直径所对的圆周角为直角,那么若 ,则
,则
 。
。
C、根据题意,由于,曲线 ,即为
,即为 为圆心,半径为
为圆心,半径为 与直线
与直线 ,即为
,即为 分别表示的为圆和直线,那么利用直线于圆的位置关系,得到弦长为
分别表示的为圆和直线,那么利用直线于圆的位置关系,得到弦长为 。
。
考点:不等式选讲,参数方程,几何证明
点评:解决的关键是对于均值不等式的运用,以及极坐标方程的理解和运用,属于基础题。

练习册系列答案
相关题目
 满足
满足 ,则
,则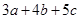 的最大值为_________.
的最大值为_________. 的直角边
的直角边 为直径的圆
为直径的圆 交
交 边于点
边于点 ,点
,点 在
在 上,且
上,且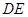 与圆
与圆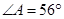 ,则
,则 _________.
_________. 与直线
与直线 的两个交点之间的距离为_________.
的两个交点之间的距离为_________.