题目内容
已知函数![]() ,(其中常数
,(其中常数![]() )
)
(1)当![]() 时,求
时,求![]() 的极大值;
的极大值;
(2)试讨论![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(3)当![]() 时,曲线
时,曲线![]() 上总存在相异两点
上总存在相异两点![]() 、
、![]() ,使得曲线
,使得曲线![]() 在点
在点![]() 、
、![]() 处的切线互相平行,求
处的切线互相平行,求![]() 的取值范围.
的取值范围.
解(1)当![]() 时,
时,![]()
![]()
![]() …………… 1分
…………… 1分
当![]() ,
,![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴![]() 在
在![]() 和
和![]() 上单调递减,在
上单调递减,在![]() 单调递减 …… 2分
单调递减 …… 2分
故![]() …………… 3分
…………… 3分
(2)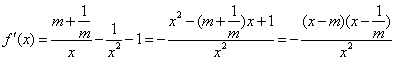
![]()
…………………………5分
①当![]() 时,则
时,则![]() ,故
,故![]() 时,
时,![]() ;
;![]() 时,
时,![]()
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增; …………… 6分
单调递增; …………… 6分
②当![]() 时,则
时,则![]() ,故
,故![]() ,有
,有![]() 恒成立,
恒成立,
此时![]() 在
在![]() 上单调递减; …………… 7分
上单调递减; …………… 7分
③当![]() 时,则
时,则![]() ,故
,故![]() 时,
时,![]() ;
;![]() 时,
时,![]()
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增; …………… 8分
单调递增; …………… 8分
(3)由题意,可得![]() (
(![]() ,且
,且![]() )
)
即 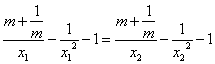
![]()
![]() …………… 9分
…………… 9分
∵![]() ,由不等式性质可得
,由不等式性质可得![]() 恒成立,又
恒成立,又![]()
∴![]()
![]()
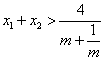 对
对![]() 恒成立 … 11分
恒成立 … 11分
令![]() ,则
,则![]()
对![]() 恒成立
恒成立
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ……………12分
……………12分
故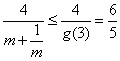 ……………………………13分
……………………………13分
从而“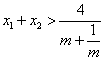 对
对![]() 恒成立”等价于“
恒成立”等价于“![]() ”
”
∴![]() 的取值范围为
的取值范围为![]()

练习册系列答案
相关题目
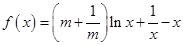 ,(其中常数
,(其中常数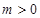 ).
). 时,求
时,求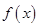 的极大值;
的极大值; 上的单调性;
上的单调性;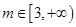 时,曲线
时,曲线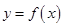 上总存在相异两点
上总存在相异两点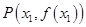 、
、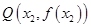 ,使得曲线
,使得曲线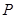 、
、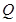 处的切线互相平行,求
处的切线互相平行,求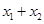 的取值范围.
的取值范围. 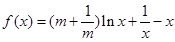 ,(其中常数
,(其中常数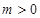 )
)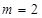 时,求
时,求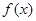 的极大值;
的极大值;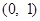 上的单调性;
上的单调性;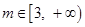 时,曲线
时,曲线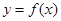 上总存在相异两点
上总存在相异两点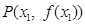 、
、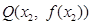 ,使得曲线
,使得曲线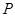 、
、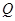 处的切线互相平行,求
处的切线互相平行,求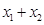 的取值范围.
的取值范围. 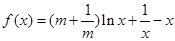 ,(其中常数
,(其中常数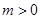 )
)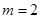 时,求
时,求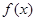 的极大值;
的极大值;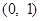 上的单调性;
上的单调性; 时,曲线
时,曲线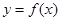 上总存在相异两点
上总存在相异两点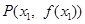 、
、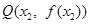 ,使得曲线
,使得曲线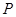 、
、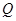 处的切线互相平行,求
处的切线互相平行,求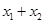 的取值范围.
的取值范围.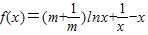 ,(其中常数m>0)
,(其中常数m>0)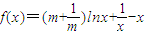 ,(其中常数m>0)
,(其中常数m>0)