题目内容
已知函数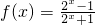 ,则不等式f(x-2)+f(x2-4)<0的解集为
,则不等式f(x-2)+f(x2-4)<0的解集为
- A.(-1,6)
- B.(-6,1)
- C.(-2,3)
- D.(-3,2)
D
分析:本题要先判出f(x)为奇函数和增函数,进而把抽象不等式转化为关于x的一元二次不等式.
解答:由题意可知f(x)的定义域为R.
∵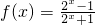
∴f(-x)+f(x)=
= =0,即f(-x)=-f(x),∴f(x)为奇函数.
=0,即f(-x)=-f(x),∴f(x)为奇函数.
又f(x)= =
= ,由复合函数的单调性可得f(x)为增函数,
,由复合函数的单调性可得f(x)为增函数,
∴f(x-2)+f(x2-4)<0可化为f(x-2)<-f(x2-4)
即f(x-2)<f(4-x2),可得x-2<4-x2,
即x2+x-6<0,解得-3<x<2,
故选D
点评:本题为函数的性质与不等式解法的结合,属中档题.
分析:本题要先判出f(x)为奇函数和增函数,进而把抽象不等式转化为关于x的一元二次不等式.
解答:由题意可知f(x)的定义域为R.
∵
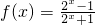
∴f(-x)+f(x)=

=
 =0,即f(-x)=-f(x),∴f(x)为奇函数.
=0,即f(-x)=-f(x),∴f(x)为奇函数.又f(x)=
 =
= ,由复合函数的单调性可得f(x)为增函数,
,由复合函数的单调性可得f(x)为增函数,∴f(x-2)+f(x2-4)<0可化为f(x-2)<-f(x2-4)
即f(x-2)<f(4-x2),可得x-2<4-x2,
即x2+x-6<0,解得-3<x<2,
故选D
点评:本题为函数的性质与不等式解法的结合,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则不等式f(x)-x≤2的解集是 .
,则不等式f(x)-x≤2的解集是 . ,则不等式f(x)-x≤2的解集是( )
,则不等式f(x)-x≤2的解集是( ) ,0]
,0]
 ,则不等式f(x)-x≤2的解集是 .
,则不等式f(x)-x≤2的解集是 . ,则不等式f(x)-x≤2的解集是 .
,则不等式f(x)-x≤2的解集是 . ,则不等式f(2-x2)+f(2x+1)>0的解集是( )
,则不等式f(2-x2)+f(2x+1)>0的解集是( )
