题目内容
(本小题满分l3分)
设椭圆![]() 的焦点分别为
的焦点分别为![]() 、
、![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)试求椭圆的方程;
(2)过![]() 、
、![]() 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于![]() 、
、![]() 、
、![]() 、
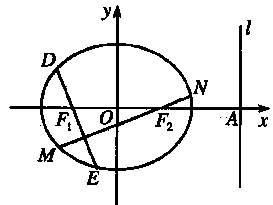
、![]() 四点(如图所示),试求四边形
四点(如图所示),试求四边形![]() 面积的最大值和最小值.
面积的最大值和最小值.
(本题12分)
解:(1)由题意,![]()
![]()
![]() 为
为![]() 的中点
的中点 ![]() 即:椭圆方程为
即:椭圆方程为![]() ………………(5分)
………………(5分)
(2)当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,此时
,此时![]() ,四边形
,四边形![]() 的面积
的面积![]() .同理当
.同理当![]() 与
与![]() 轴垂直时,也有四边形
轴垂直时,也有四边形![]() 的面积
的面积![]() . 当直线
. 当直线![]() ,
,![]() 均与
均与![]() 轴不垂直时,设
轴不垂直时,设![]() :
:![]() ,代入消去
,代入消去![]() 得:
得:![]() 设
设
所以,![]() ,所以,
,所以,![]() ,
,
同理 ……………9分
……………9分
所以四边形的面积

令![]()
因为![]() 当
当![]() ,
,
且S是以u为自变量的增函数,所以![]() .
.
综上可知,![]() .故四边形
.故四边形![]() 面积的最大值为4,最小值为
面积的最大值为4,最小值为![]() .…(13分)
.…(13分)


练习册系列答案
相关题目
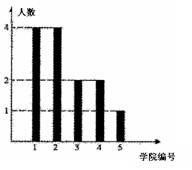
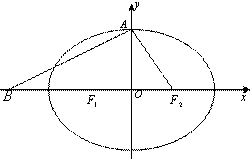 (3)在(2)的条件下,过右焦点
(3)在(2)的条件下,过右焦点 (3)在(2)的条件下,过右焦点
(3)在(2)的条件下,过右焦点