题目内容
设f(x)=asinωx+bcosωx(ω>0)的周期T=π,最大值为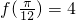 ,
,
(1)求ω、a、b的值;
(2)若α、β为方程f(x)=0的两根,且α、β的终边不共线,求tan(α+β)的值.
解:(1)f(x)= sin(ωx+?),
sin(ωx+?),
∴T=π,∴ 又f(x)的最大值为
又f(x)的最大值为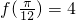 .
.
∴4= ①,且4=asin
①,且4=asin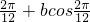 ②,
②,
由①、②解出a=2,b=3.
(2)f(x)=2sin2x+2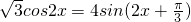 ,
,
∴f(α)=f(β)=0,
∴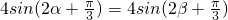 ,
,
∴2α+ ,或2α+
,或2α+ ,
,
即α=kπ+β(α、β共线,故舍去),或α+β=kπ+ ,
,
∴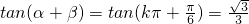 (k∈Z).
(k∈Z).
分析:(1)利用辅助角公式可把已知化简,f(x)=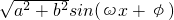 ,由周期T=π,代入周期公式T=
,由周期T=π,代入周期公式T= 可求ω,又f(x)的最大值为
可求ω,又f(x)的最大值为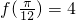 .可得
.可得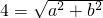 ①,且
①,且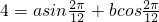 ②,联立可解a,b
②,联立可解a,b
(2)由(1)可得f(x)=4sin(2x+ ),由f(α)=f(β)=0?
),由f(α)=f(β)=0?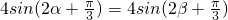 ,
,
从而有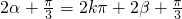 ,或
,或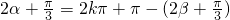 ,整理代入可求
,整理代入可求
点评:本题考查了三角函数的辅助角asinx+bcosx=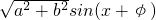 的运用,周期公式T=
的运用,周期公式T= 的应用,三角函数的最值的求解,及三角方程的求解,综合的知识比较多,要求考生要熟练掌握三角函数的相关性质,才能熟练解题.
的应用,三角函数的最值的求解,及三角方程的求解,综合的知识比较多,要求考生要熟练掌握三角函数的相关性质,才能熟练解题.
 sin(ωx+?),
sin(ωx+?),∴T=π,∴
 又f(x)的最大值为
又f(x)的最大值为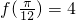 .
.∴4=
 ①,且4=asin
①,且4=asin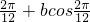 ②,
②,由①、②解出a=2,b=3.
(2)f(x)=2sin2x+2
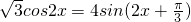 ,
,∴f(α)=f(β)=0,
∴
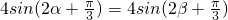 ,
,∴2α+
 ,或2α+
,或2α+ ,
,即α=kπ+β(α、β共线,故舍去),或α+β=kπ+
 ,
,∴
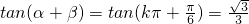 (k∈Z).
(k∈Z).分析:(1)利用辅助角公式可把已知化简,f(x)=
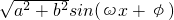 ,由周期T=π,代入周期公式T=
,由周期T=π,代入周期公式T= 可求ω,又f(x)的最大值为
可求ω,又f(x)的最大值为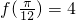 .可得
.可得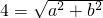 ①,且
①,且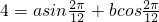 ②,联立可解a,b
②,联立可解a,b(2)由(1)可得f(x)=4sin(2x+
 ),由f(α)=f(β)=0?
),由f(α)=f(β)=0?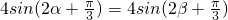 ,
,从而有
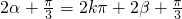 ,或
,或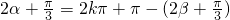 ,整理代入可求
,整理代入可求点评:本题考查了三角函数的辅助角asinx+bcosx=
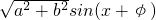 的运用,周期公式T=
的运用,周期公式T= 的应用,三角函数的最值的求解,及三角方程的求解,综合的知识比较多,要求考生要熟练掌握三角函数的相关性质,才能熟练解题.
的应用,三角函数的最值的求解,及三角方程的求解,综合的知识比较多,要求考生要熟练掌握三角函数的相关性质,才能熟练解题. 
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目