题目内容
(2012年高考(江苏))已知各项均为正数的两个数列![]() 和
和![]() 满足:
满足: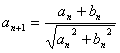 ,
,![]() ,
,
(1)设![]() ,
,![]() ,求证:数列
,求证:数列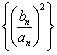 是等差数列;
是等差数列;
(2)设![]() ,
,![]() ,且
,且![]() 是等比数列,求
是等比数列,求![]() 和
和![]() 的值.
的值.![]()
【答案】解:(1)∵![]() ,∴
,∴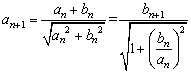 .
.
∴ 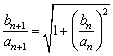 .∴
.∴  .
.
∴数列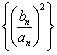 是以1 为公差的等差数列.
是以1 为公差的等差数列.
(2)∵![]() ,∴
,∴![]() .
.
∴![]() .(﹡)
.(﹡)
设等比数列![]() 的公比为
的公比为![]() ,由
,由![]() 知
知![]() ,下面用反证法证明
,下面用反证法证明![]()
若![]() 则
则![]() ,∴当
,∴当![]() 时,
时,![]() ,与(﹡)矛盾.
,与(﹡)矛盾.
若![]() 则
则![]() ,∴当
,∴当![]() 时,
时,![]() ,与(﹡)矛盾.
,与(﹡)矛盾.
∴综上所述,![]() .∴
.∴![]() ,∴
,∴![]() .
.
又∵![]()
![]() ,∴
,∴![]() 是公比是
是公比是![]() 的等比数列.
的等比数列.
若![]() ,则
,则![]() ,于是
,于是![]() .
.
又由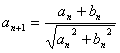 即
即![]() ,得
,得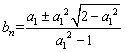 .
.
∴![]() 中至少有两项相同,与
中至少有两项相同,与![]() 矛盾.∴
矛盾.∴![]() .
.
∴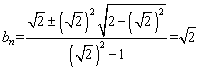 .
.
∴ ![]() .
.
【考点】等差数列和等比数列的基本性质,基本不等式,反证法.
【解析】(1)根据题设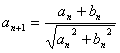 和
和![]() ,求出
,求出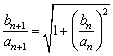 ,从而证明
,从而证明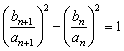 而得证.
而得证.
(2)根据基本不等式得到![]() ,用反证法证明等比数列
,用反证法证明等比数列![]() 的公比
的公比![]() .
.
从而得到![]() 的结论,再由
的结论,再由![]() 知
知![]() 是公比是
是公比是![]() 的等比数列.最后用反证法求出
的等比数列.最后用反证法求出![]() .
.

练习册系列答案
相关题目