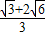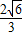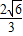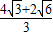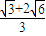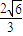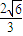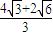题目内容
12.将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为（A）
（B）2+
（C）
（D）
C
解析：当4个钢球彼此相切、且与正四面体的容器的各面均相切时，正四面体的高取最小值.
底面球心R1在底面上的投影为R1′，过R1′作GE∥CD交BC、BO于点E、G.在AB上截取BF=BE=BG.得小正四面体B—EFG.R1′是G上的中点，R1B垂直底面EFG，R1′H=BR1′，
在Rt△BHR1′中，R1′H=
BH.
=
=
，
∴BR1′=2
R1′R=2
.
在底面BCD中，球心R1R2R3投影如上图，据正四面体及球心对称性知∠MBR1′=30°，
BM=
BR1′=
·2
=
.
大正四面体的边长为2+2
.
斜高h′=
BC=3
+
，
高h=
=
h′=4+
.
练习册系列答案
初中暑期衔接系列答案
相关题目
将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为（ ）
A、
| ||||||
B、2+
| ||||||
C、4+
| ||||||
D、
|
