题目内容
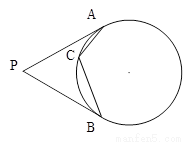
如图，已知PA、PB是圆O的切线，A、B分别为切点，C为圆O上不与A、B重合的另一点，若∠ACB = 120°，则∠APB =
【答案】
120度
【解析】解：解：连接OA，OB，根据切线的性质定理以及四边形的内角和定理得：∠AOB=180°-120°=60°，
则利用圆周角定理，可得∠APB =120度
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
开心快乐假期作业暑假作业西安出版社系列答案名题训练系列答案
如图，已知PA⊥α，PB⊥β，垂足分别是A，B，且α∩β=l，．
如图，已知PA、PB是圆O的切线，A、B分别为切点，C为圆O上不与A、B重合的另一点，若∠ACB=120°，则∠APB=
如图，已知PA⊥α，PB⊥β，垂足分别是A，B，且α∩β=l，．
，判断平面α与平面β的位置关系，并给出证明．