题目内容
已知函数![]() 。
。
(Ⅰ)解不等式![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
(Ⅰ)f(x)+f(x+4)=|x-1|+|x+3|=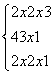
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3.
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}.
(Ⅱ)f(ab)>|a|f(![]() )即|ab-1|>|a-b|.
)即|ab-1|>|a-b|.
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.
故所证不等式成立.

练习册系列答案
相关题目
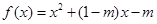
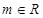 ,解不等式
,解不等式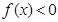 ;
;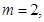 解不等式
解不等式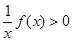
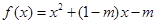
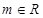 ,解不等式
,解不等式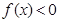 ;
;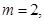 解不等式
解不等式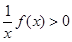
 不等式
不等式 的解集为
的解集为
 对一切实数x恒成立,求实数c的取值范围。
对一切实数x恒成立,求实数c的取值范围。
 的不等式
的不等式
 的图象恒在函数
的图象恒在函数 的图象上方,求实数
的图象上方,求实数 的取值范围。
的取值范围。 .
. ≤4;(Ⅱ)若存在x使得
≤4;(Ⅱ)若存在x使得 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围.