题目内容
三棱锥S-ABC的三条侧棱两两垂直，SA=5，SB=4，SC=3，D为AB中点，E为AC中点，求四棱锥S-BCED的体积．
解：∵D、E分别是AB、AC中点，
∴S△ADE=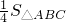
，∴
，∴
，
∵AS⊥BS，AS⊥CS，BS∩CS=S，
∴AS⊥面BSC∴
，
∴
．
分析：求四棱锥S-BCED的体积，转化为求，求三棱锥S-ABC的体积，即可求出结果．
点评：本题考查几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．
∴S△ADE=
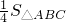，∴，∴，∵AS⊥BS，AS⊥CS，BS∩CS=S，
∴AS⊥面BSC∴
，∴
．分析：求四棱锥S-BCED的体积，转化为求
，求三棱锥S-ABC的体积，即可求出结果．点评：本题考查几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．
练习册系列答案
相关题目
如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积．