题目内容
已知三角形的三边长分别为 ,
,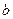 ,
, ,内切圆的半径为
,内切圆的半径为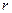 ;则三角形的面积为
;则三角形的面积为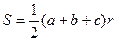 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 .类比三角形的面积可得四面体的体积为( )
.类比三角形的面积可得四面体的体积为( )
A.   | B.   |
C.   | D.   |
B
解析

练习册系列答案
相关题目
一个空间四边形 的四条边及对角线
的四条边及对角线 的长均为
的长均为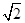 ,二面角
,二面角 的余弦值为
的余弦值为 ,则下列论断正确的是
,则下列论断正确的是
A.空间四边形 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为 |
B.空间四边形 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为 |
C.空间四边形 的四个顶点在同一球面上且此球的表面积为 的四个顶点在同一球面上且此球的表面积为 |
D.不存在这样的球使得空间四边形 的四个顶点在此球面上 的四个顶点在此球面上 |
设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为
A.3 a2 a2 | B.6 a2 a2 | C.12 a2 a2 | D.24 a2 a2 |
一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 ( )
A. ; ; | B. ; ; | C. ; ; | D. . . |
用与球心距离为1的平面去截球,所得的截面面积为π,则球的休积为
A. | B. | C. | D. |
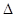 ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且  ,BC=1,AC=3,三棱锥O- ABC的体积为
,BC=1,AC=3,三棱锥O- ABC的体积为  ,则球O的表面积为__________。
,则球O的表面积为__________。 、
、 、
、 .则三棱锥A—BCD的外接球的体积为
.则三棱锥A—BCD的外接球的体积为 B.
B.

 D.
D.
 ,四个顶点在同一个球面上,则此球的表面积为
,四个顶点在同一个球面上,则此球的表面积为 B.
B. C.
C. D
D .3
.3