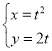题目内容
【题目】在直角坐标系xOy中，曲线C1：
，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C2是圆心极坐标为（3，π），半径为1的圆.
（1）求曲线C1的参数方程和C2的直角坐标方程；
（2）设M，N分别为曲线C1，C2上的动点，求|MN|的取值范围.
【答案】（1）
（φ为参数）；（x+3）2+y2＝1（2）[1，5]
【解析】
（1）由曲线
，能求出
的参数方程；求出曲线
是圆心直角坐标为
，半径为1的圆，由此能求出的直角坐标方程；（2）设
，
，则
，由此能求出
的取值范围．
（1）∵曲线C1：
，
∴C1的参数方程为
（φ为参数），
∵曲线C2是圆心极坐标为（3，π），半径为1的圆，
∴曲线C2是圆心直角坐标为（﹣3，0），半径为1的圆，
∴C2的直角坐标方程为（x+3）2+y2＝1.
（2）设M（cosφ，2sinφ），C2（﹣3，0），
∴
3cos2φ+6cosφ+13＝﹣3（cosφ﹣1）2+16，
∵﹣1≤cosφ≤1，∴
，2≤|MC2|≤4，
∴1≤|MN|≤5.
∴|MN|的取值范围是[1，5].
练习册系列答案
孟建平名校考卷系列答案
相关题目
