题目内容

（2011•潍坊二模）
∫
π
2
0
(x-sinx)dx等于（　　）
分析：由于F（x）=
1
2
x2+cosx为f（x）=x-sinx的一个原函数即F′（x）=f（x），根据∫abf（x）dx=F（x）|ab公式即可求出值．
解答：解：∵（
1
2
x2+cosx）′=x-sinx，
∴
∫
π
2
0
(x-sinx)dx=（
1
2
x2+cosx）|
 
π
2
0
=
π3
8
-1
故答案为：B
点评：此题考查学生掌握函数的求导法则，会求函数的定积分运算，是一道基础题
练习册系列答案
相关题目
（2011•潍坊二模）设p：
xx-2
＜0，q：0＜x＜m，若p是q成立的充分不必要条件，则m的取值范围是
（2，+∞）
（2，+∞）
．
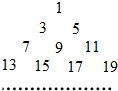（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是
101
101
．
（2011•潍坊二模）已知
m
=(cos?x，sin?x)，
n
=(cos?x，2
3
cos?x-sin?x)，?＞0，函数f(x)=
m
•
n
+|
m
|，x1，x2是集合M={x|f（x）=1}中任意两个元素，且|x1-x2|的最小值为
π
2
．
（1）求?的值．
（2）在△ABC中，a，b，c分别是A，B，C的对边．f(A)=2，c=2，S△ABC=
3
2
，求a的值．
（2011•潍坊二模）运行如图的程序框图，当输入m=-4时的输出结果为n，若变量x，y满足
x+y≤3
x-y≥-1
y≥n
，则目标函数z=2x+y的最大值为
5
5
．
（2011•潍坊二模）已知偶函数f（x）对?x∈R满足f（2+x）=f（2-x）且当-2≤x≤0时，f（x）=log2（1-x），则f（2011）的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网