题目内容
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
α+β=A,α-β=B 有α=
 ,β=
,β=
代入③得 sinA+cosB=2sin
 cos
cos .
.(1)类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
 sin
sin ;
;(2)若△ABC的三个内角A,B,C满足cos2A+cox2C-cos2B=1,直接利用阅读材料及(1)中的结论试判断△ABC的形状.
【答案】分析:(1)通过两角和与差的余弦公式,令α+β=A,α-β=B有α= ,β=
,β= ,即可证明结果.
,即可证明结果.
(2)利用(1)中的结论和二倍角公式,cos2A-cos2B=2sin2C,以及A+B+C=π,推出2sinAcosB=0.∠B= .得到△ABC为直角三角形.
.得到△ABC为直角三角形.
解答:解:(1)证明:因为cos(α+β)=cosαcosβ-sinαsinβ,------①
cos(α-β)=cosαcosβ+sinαsinβ②
①-②得cos(α+β)-cos(α-β)=-2sinαsinβ③…
令α+β=A,α-β=B有α= ,β=
,β= ,
,
代入③得cosA-cosB=-2sin sin
sin ..…(8分)
..…(8分)
(2)由cos2A+cox2C-cos2B=1得:cos2A-cos2B=2sin2C.
由(1)中结论得:-2sin(A+B)sin(A-B)=2sin2C,
因为A,B,C为△ABC的内角,所以A+B+C=π,
所以-sin(A+B)sin(A-B)=sin2(A+B).
又因为0<A+B<π,所以sin(A+B)≠0,
所以sin(A+B)+sin(A-B)=0.
从而2sinAcosB=0.…(10分)
又因为sinA≠0,所以cosB=0,即∠B= .
.
所以△ABC为直角三角形.…(12分)
点评:本小题主要考查两角和与差三角函数公式、二倍角公式、三角函数的恒等变换等基础知识,考查推理论证能力,运算求解能力,考查化归与转化思想等.
 ,β=
,β= ,即可证明结果.
,即可证明结果.(2)利用(1)中的结论和二倍角公式,cos2A-cos2B=2sin2C,以及A+B+C=π,推出2sinAcosB=0.∠B=
 .得到△ABC为直角三角形.
.得到△ABC为直角三角形.解答:解:(1)证明:因为cos(α+β)=cosαcosβ-sinαsinβ,------①
cos(α-β)=cosαcosβ+sinαsinβ②
①-②得cos(α+β)-cos(α-β)=-2sinαsinβ③…
令α+β=A,α-β=B有α=
 ,β=
,β= ,
,代入③得cosA-cosB=-2sin
 sin
sin ..…(8分)
..…(8分)(2)由cos2A+cox2C-cos2B=1得:cos2A-cos2B=2sin2C.
由(1)中结论得:-2sin(A+B)sin(A-B)=2sin2C,
因为A,B,C为△ABC的内角,所以A+B+C=π,
所以-sin(A+B)sin(A-B)=sin2(A+B).
又因为0<A+B<π,所以sin(A+B)≠0,
所以sin(A+B)+sin(A-B)=0.
从而2sinAcosB=0.…(10分)
又因为sinA≠0,所以cosB=0,即∠B=
 .
.所以△ABC为直角三角形.…(12分)
点评:本小题主要考查两角和与差三角函数公式、二倍角公式、三角函数的恒等变换等基础知识,考查推理论证能力,运算求解能力,考查化归与转化思想等.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
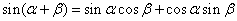 ----------①
----------①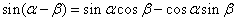 ------②
------②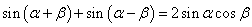 ------③
------③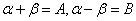 有
有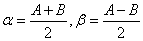
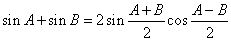 .
.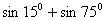 的值。
的值。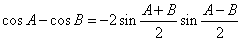 ;
;