题目内容

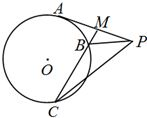
建立极坐标系证明：已知半圆直径|AB|=2（>0），半圆外一条直线与AB所在直线垂直相交于点T，并且∣AT|=2.若半圆上相异两点M.N到的距离|MP|，|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1，则|MA|+|NA|=|AB|.　

略


解析:

证法一：以A为极点，射线AB为极轴建立直角坐标系，则半圆的的极坐标方程为，设，则，，又，，

 

是方程的两个根，由韦达定理：，

证法二：以A为极点，射线AB为极轴建立直角坐标系，则半圆的的极坐标方程为，设,又由题意知，在抛物线上，，，是方程的两个根，由韦达定理：，

练习册系列答案
相关题目
精英家教网选做题本题包括A，B，C，D四小题，请选定其中 两题 作答，每小题10分，共计20分，
解答时应写出文字说明，证明过程或演算步骤．
A选修4-1：几何证明选讲
自圆O外一点P引圆的一条切线PA，切点为A，M为PA的中点，过点M引圆O的割线交该圆于B、C两点，且∠BMP=100°，∠BPC=40°，求∠MPB的大小．
B选修4-2：矩阵与变换
已知二阶矩阵A=
ab
cd
，矩阵A属于特征值λ1=-1的一个特征向量为α1=
1
-1
，属于特征值λ2=4的一个特征向量为α2=
3
2
．求矩阵A．
C选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C的参数方程为
x=2cosα
y=sinα
(α为参数)．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ-
π
4
)=2
2
．点
P为曲线C上的动点，求点P到直线l距离的最大值．
D选修4-5：不等式选讲
若正数a，b，c满足a+b+c=1，求
1
3a+2
+
1
3b+2
+
1
3c+2
的最小值．
（2013•宿迁一模）【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，已知AB，CD是圆O的两条弦，且AB是线段CD的 垂直平分线，若AB=6，CD=2
5
，求线段AC的长度．
B．选修4-2：矩阵与变换（本小题满分10分）
已知矩阵M=
21
1a
的一个特征值是3，求直线x-2y-3=0在M作用下的新直线方程．
C．选修4-4：坐标系与参数方程（本小题满分10分）
在平面直角坐标系xOy中，已知曲线C的参数方程是
x=cosα
y=sinα+1
（α是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程．
D．选修4-5：不等式选讲（本小题满分10分）
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R，求正实数a的取值范围．
（A）（不等式选做题）不等式|x+1|-|x-2|＞2的解集为
(
3
2
，+∞)
(
3
2
，+∞)
．
（B）（几何证明选做题）如图，已知Rt△ABC的两条直角边AC，BC的长分别为6cm，8cm，以AC为直径的圆与AB交于点D，则AD=
18
5
(或3.6)
18
5
(或3.6)
cm．
（C）（坐标系与参数方程选做题）圆C的参数方程
x=1+cosα
y=1-sinα
（α为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρsinθ=1，则直线l与圆C的交点的直角坐标是
（0，1），或（2，1）
（0，1），或（2，1）
．
附加题：（选做题：在下面A、B、C、D四个小题中只能选做两题）
A．选修4-1：几何证明选讲
如图，已知AB、CD是圆O的两条弦，且AB是线段CD的垂直平分线，
已知AB=6，CD=2
5
，求线段AC的长度．
B．选修4-2：矩阵与变换
已知二阶矩阵A有特征值λ1=1及对应的一个特征向量e1=
1
1
和特征值λ2=2及对应的一个特征向量e2=
1
0
，试求矩阵A．
C．选修4-4：坐标系与参数方程
在直角坐标系xOy中，已知曲线C的参数方程是
y=sinθ+1
x=cosθ
（θ是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程．
D．选修4-5：不等式选讲
已知关于x的不等式|ax-1|+|ax-a|≥1（a＞0）．
（1）当a=1时，求此不等式的解集；
（2）若此不等式的解集为R，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网