题目内容
已知
，则k的取值范围________．
分析：先由题意作出图形，由题意可得两集合分别表示的图形是阴影部分及圆．根据题意得只要直线与已知圆相切或相离即可
解答：
解：由于直线y=kx+4恒过定点A（0，4），作出不等式组表示的平面区域，如图所示∵
直线y=kx+4与圆x2+y2=4相切或相离
∴
∴
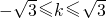
故答案为：[-
，]点评：本小题主要考查二元一次不等式（组）与平面区域、圆方程的综合应用、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
已知圆C：x2+y2-4x-2y+1=0，直线l：3x-4y+k=0圆上存在两点到直线l的距离为1，则k的取值范围是（ ）
| A、（-17，-7） | B、（3，13） | C、（-17，-7）∪（3，13） | D、[-17，-7]∪[3，13] |
已知f（x）是以2为周期的偶函数，当x∈[0，1]时，f（x）=x，那么在区间[-1，3]内，关于x的方程f（x）=kx+k+1（k∈R且k≠-1）有4个不同的根，则k的取值范围是（ ）
A、(-
| ||
| B、（-1，0） | ||
C、(-
| ||
D、(-
|
，则k的取值范围 ．