题目内容
已知二次函数f(x)＝x2－2ax＋4，求在下列条件下，实数a的取值范围．
(1)零点均大于1；
(2)一个零点大于1，一个零点小于1；
(3)一个零点在(0,1)内，另一个零点在(6,8)内．
解析： (1)因为方程x2－2ax＋4＝0的两根均大于1，结合二次函数的单调性与零点存在性定理得
解得2≤a<
.
(2)因为方程x2－2ax＋4＝0的一个根大于1，一个根小于1，结合二次函数的单调性与零点存在性定理得f(1)＝5－2a<0，解得a>.
(3)因为方程x2－2ax＋4＝0的一个根在(0,1)内，另一个根在(6,8)内，结合二次函数的单调性与零点存在性定理得
解得
<a<
.
练习册系列答案
阅读快车系列答案
相关题目
求不等式f(x)>2的解集．
若函数f(x)＝x3＋x2－2x－2的一个零点(正数)附近的函数值用二分法逐次计算，参考数据如下表：
| f(1)＝－2 | f(1.5)＝0.625 |
| f(1.25)≈－0.984 | f(1.375)≈－0.260 |
| f(1.437 5)≈0.162 | f(1.406 25)≈－0.054 |
那么方程x3＋x2－2x－2＝0的一个近似解(精确度0.04)为________．
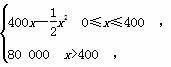
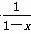的一个零点．若x1∈(1，x0)，x2∈(x0，＋∞)，则( )
