题目内容
{an},{bn}都是各项为正数的数列,对任意的自然数n,都有an、bn2、an+1成等差数列,bn2、an+1、bn+12成等比数列.
(1)试问{bn}是否是等差数列?为什么?
(2)求证:对任意的自然数p,q(p>q),bp-q2+bp+q2≥2bp2成立;
(3)如果a1=1,b1=![]() ,Sn=
,Sn=![]() ,求
,求![]() .
.
答案:
解析:
解析:
|
是等差数列;;2 依题意2bn2=an+an+1, ① an+12=bn2·bn+12. ② (1)∵an>0,bn>0,∴由②式得an+1=bn·bn+1,从而n≥2时,an=bn-1·bn,代入①2bn2= bn-1bn+bnbn+1, ∴2bn=bn-1+bn+1(n≥2), ∴{bn}是等差数列. (2)因为{bn}是等差数列,∴bp-q+bp+q=2bp. ∴bp-q2+bp+q2≥ (3)由a1=1,b1= ∴{bn}中公差d= ∴bn=b1+(n-1)d = ∴an+1= 又a1=1也适合③,∴an= ∴ ∴Sn=2[1- =2(1- ∴ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线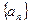 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)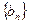 的通项公式;
的通项公式; 问是否存在k
问是否存在k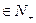 ,使得f(k+5)=2f(k)-2成立;若存在,求出
,使得f(k+5)=2f(k)-2成立;若存在,求出 k的值,若不存在,说明理由。
k的值,若不存在,说明理由。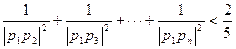 (n≥2,n∈N+)
(n≥2,n∈N+)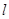 :y=2x+2上,P1为直线
:y=2x+2上,P1为直线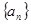 成等差数列,公差为1.(n∈N+)
成等差数列,公差为1.(n∈N+)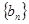 的通项公式;
的通项公式;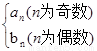 问是否存在k
问是否存在k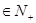 ,使得f(k+5)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由。
,使得f(k+5)=2f(k)-2成立;若存在,求出k的值,若不存在,说明理由。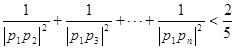 (n≥2,n∈N+)
(n≥2,n∈N+)