题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.已知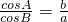 ,且
,且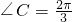 .
.
(Ⅰ)求角A,B的大小;
(Ⅱ)设函数f(x)=sin(x+A)+cosx,求f(x)在[-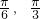 ]上的最大值.
]上的最大值.
解:(Ⅰ)∵已知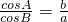 ,由正弦定理得
,由正弦定理得 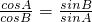 ,即 sin2A=sin2B. …(3分)
,即 sin2A=sin2B. …(3分)
∴A=B,或A+B= (舍去),∴C=
(舍去),∴C= ,则A=B=
,则A=B= . …(6分)
. …(6分)
(Ⅱ)∵函数f(x)=sin(x+A)+cosx=sin(x+ )+cosx=
)+cosx= sin(x+
sin(x+ ),…(10分)
),…(10分)
∵x∈[-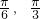 ],则
],则  ≤x+
≤x+ ≤
≤ . …(12分)
. …(12分)
故当 x+ =
= 时,函数f(x)=
时,函数f(x)= sin(x+
sin(x+ )取得最大值为
)取得最大值为  . …(14分)
. …(14分)
分析:(Ⅰ)由已知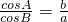 ,利用正弦定理求得 sin2A=sin2B,故A=B,再由 C=
,利用正弦定理求得 sin2A=sin2B,故A=B,再由 C= ,可得A和B的值.
,可得A和B的值.
(Ⅱ)化简函数f(x)为 sin(x+
sin(x+ ),根据x∈[-
),根据x∈[-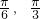 ],可得
],可得  ≤x+
≤x+ ≤
≤ ,由此求得f(x)的最大值.
,由此求得f(x)的最大值.
点评:本题主要考查正弦定理、余弦定理及三角运算等基础知识,两角和差的正弦公式,同时考查运算求解能力,属于中档题.
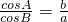 ,由正弦定理得
,由正弦定理得 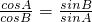 ,即 sin2A=sin2B. …(3分)
,即 sin2A=sin2B. …(3分)∴A=B,或A+B=
 (舍去),∴C=
(舍去),∴C= ,则A=B=
,则A=B= . …(6分)
. …(6分)(Ⅱ)∵函数f(x)=sin(x+A)+cosx=sin(x+
 )+cosx=
)+cosx= sin(x+
sin(x+ ),…(10分)
),…(10分)∵x∈[-
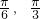 ],则
],则  ≤x+
≤x+ ≤
≤ . …(12分)
. …(12分)故当 x+
 =
= 时,函数f(x)=
时,函数f(x)= sin(x+
sin(x+ )取得最大值为
)取得最大值为  . …(14分)
. …(14分)分析:(Ⅰ)由已知
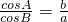 ,利用正弦定理求得 sin2A=sin2B,故A=B,再由 C=
,利用正弦定理求得 sin2A=sin2B,故A=B,再由 C= ,可得A和B的值.
,可得A和B的值.(Ⅱ)化简函数f(x)为
 sin(x+
sin(x+ ),根据x∈[-
),根据x∈[-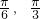 ],可得
],可得  ≤x+
≤x+ ≤
≤ ,由此求得f(x)的最大值.
,由此求得f(x)的最大值.点评:本题主要考查正弦定理、余弦定理及三角运算等基础知识,两角和差的正弦公式,同时考查运算求解能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |