题目内容
已知B、C两点在双曲线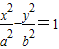
（a＞0，b＞0）上，且关于中心O对称，焦点F1和B点都在y轴的右侧，
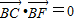且|
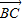|=2|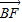
|，则双曲线的离心率是（ ）A．2+
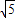
B．3+
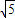
C．
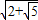
D．
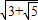
【答案】分析：由B、C两点关于中心O对称，|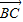
|=2|
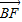|，及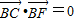
可判断△OBF为等腰直角三角形，结合OF=c，可得B点坐标，代入构造关于e的方程，解方程可得答案．
解答：解：∵B、C两点关于中心O对称，|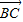
|=2|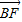
|，
∴BO=BF
又∵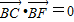
∴BC⊥BF
即△OBF为等腰直角三角形
故B点坐标为（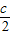
，
）
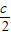代入双曲线方程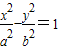
得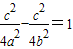
即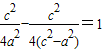
即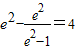
即e4-6e2+4=0
解得e2=3+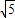
或e2=3-
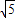（舍去）
∴e=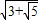
故选D
点评：本题考查的知识点是双曲线的简单性质，其中根据，|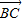
|=2|
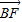|，及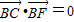
可判断△OBF为等腰直角三角形，进而求出B点坐标是解答的关键．
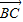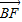|=2||，及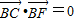可判断△OBF为等腰直角三角形，结合OF=c，可得B点坐标，代入构造关于e的方程，解方程可得答案．解答：解：∵B、C两点关于中心O对称，|
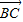|=2|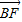|，∴BO=BF
又∵
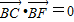
∴BC⊥BF
即△OBF为等腰直角三角形
故B点坐标为（
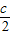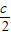，）代入双曲线方程
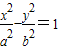得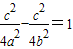即
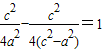
即
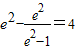
即e4-6e2+4=0
解得e2=3+
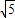或e2=3-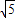（舍去）∴e=
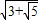
故选D
点评：本题考查的知识点是双曲线的简单性质，其中根据，|
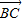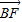|=2||，及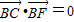可判断△OBF为等腰直角三角形，进而求出B点坐标是解答的关键． 
练习册系列答案
相关题目
一条渐近线的方程是
过双曲线C的右焦点F2的一条弦交双曲线右支于P、Q两点，R是弦PQ的中点.
|F1F2|，求线段AB的中点M的迹方程，并说明该轨迹是什么曲线。
，当点P在曲线C上运动时，求a的取值范围.
)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．