Question

在△ABC中，AB=BC，∠B=120°，若以A、B为焦点的椭圆经过点C，则该椭圆的离心率e=________．

Answer 1

分析：先计算AC的长，再利用以A、B为焦点的椭圆经过点C，即可求得椭圆的离心率．
解答：设AB=BC=1，则AC²=AB²+BC²-2AB•BC•cosB=1+1-2×1×1×=3
∴AC=
∵以A、B为焦点的椭圆经过点C，
∴2a=，2c=1
∴e===
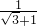故答案为：
点评：本题考查余弦定理的运用，考查椭圆的几何性质，属于基础题．