题目内容
已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（ ）A．（
，
p）B．（
，
p）C．（
，
p）D．（
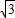p，
）
【答案】分析：设M（x，y）根据定义点M与焦点F的距离等于M到准线的距离得出x+
=2P，即可求出x，然后代入抛物线方程求出y即可求出坐标．
解答：解：根据定义，点M与准线的距离也是2P，
设M（x，y），则M与准线的距离为：x+
∴x+
=2P，x=
，
∴y=
P，
∴点M的坐标 （
，
P）
故选A．
点评：本题考查了抛物线的定义和性质，解题的关键是根据定义得出点M与焦点F的距离等于M到准线的距离，属于基础题．
=2P，即可求出x，然后代入抛物线方程求出y即可求出坐标．解答：解：根据定义，点M与准线的距离也是2P，
设M（x，y），则M与准线的距离为：x+
∴x+=2P，x=，∴y=
P，∴点M的坐标 （
，P）故选A．
点评：本题考查了抛物线的定义和性质，解题的关键是根据定义得出点M与焦点F的距离等于M到准线的距离，属于基础题．
练习册系列答案
相关题目
已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（ ）
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|