��Ŀ����
��֪����C��f��x��=x2��C�ϵĵ�A0��An�ĺ�����ֱ�Ϊ1��an��n��N*������a1=5������{xn}���� ��������Dn=[1��an]��an��1������x��Dnʱ������C�ϴ��ڵ�Pn��xn��f��xn������ʹ�õ�Pn����������ֱ��A0Anƽ�У�
��������Dn=[1��an]��an��1������x��Dnʱ������C�ϴ��ڵ�Pn��xn��f��xn������ʹ�õ�Pn����������ֱ��A0Anƽ�У�
��1��֤����{logt��xn-1��+1}�ǵȱ����У�
��2����Dn+1?Dn��һ��n��N*�����ʱ����t��ȡֵ��Χ��
��3��������{an}��ǰn���ΪSn����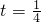 ʱ���ԱȽ�Sn��n+7�Ĵ�С����֤����Ľ��ۣ�
ʱ���ԱȽ�Sn��n+7�Ĵ�С����֤����Ľ��ۣ�
�⣺��1���������ڵ�Pn��������ֱ��AAnƽ�У�
�� ����
���� ��
��
��xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2��
��logt��xn+1-1��=1+2logt��xn-1����
��logt��xn+1-1��+1=2[logt��xn-1��+1]��
��{logt��xn-1��+1}������Ϊlogt2+1������Ϊ2�ĵȱ����У�
��2���ɣ�1����logt��xn-1��+1=��logt2+1��•2n-1��
�� ��
��
�Ӷ� ��
��
��Dn+1?Dn��һ��n��N*�������
��an+1��an��
�� ��
��
��0��2t��1��
��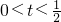 ��
��
��3����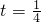 ʱ��
ʱ�� ��
��
�� ��
��
��n��3ʱ��2n-1��n+1��
��n��4ʱ��2n-1��n+1��
�൱n��3ʱ�� ��n+7��
��n+7��
��n��4ʱ��Sn��

=
��n+7��
�����������������n��N*������Sn��n+7��
��������1�������ڵ�Pn��������ֱ��AAnƽ�У�֪ ����xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2���ɴ��ܹ�֤��{logt��xn-1��+1}�ǵȱ����У�
����xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2���ɴ��ܹ�֤��{logt��xn-1��+1}�ǵȱ����У�
��2����logt��xn-1��+1=��logt2+1��•2n-1���� ���Ӷ�
���Ӷ� ����Dn+1?Dn��һ��n��N*���������an+1��an���ɴ������t��ȡֵ��Χ��
����Dn+1?Dn��һ��n��N*���������an+1��an���ɴ������t��ȡֵ��Χ��
��3����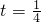 ʱ��
ʱ�� ������
������ ���ɴ��ܹ��ȽϱȽ�Sn��n+7�Ĵ�С��
���ɴ��ܹ��ȽϱȽ�Sn��n+7�Ĵ�С��
���������⿼�������벻��ʽ���ۺ����ã�����ʱҪ�������⣬��ϸ���ע���ھ������е����������������ؽ��еȼ�ת����
��
 ����
���� ��
����xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2��
��logt��xn+1-1��=1+2logt��xn-1����
��logt��xn+1-1��+1=2[logt��xn-1��+1]��
��{logt��xn-1��+1}������Ϊlogt2+1������Ϊ2�ĵȱ����У�
��2���ɣ�1����logt��xn-1��+1=��logt2+1��•2n-1��
��
 ��
���Ӷ�
 ��
����Dn+1?Dn��һ��n��N*�������
��an+1��an��
��
 ��
����0��2t��1��
��
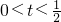 ��
����3����
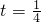 ʱ��
ʱ�� ��
����
 ��
����n��3ʱ��2n-1��n+1��
��n��4ʱ��2n-1��n+1��
�൱n��3ʱ��
 ��n+7��
��n+7����n��4ʱ��Sn��


=

��n+7��
�����������������n��N*������Sn��n+7��
��������1�������ڵ�Pn��������ֱ��AAnƽ�У�֪
 ����xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2���ɴ��ܹ�֤��{logt��xn-1��+1}�ǵȱ����У�
����xn+1=tf��xn+1-1��+1����xn+1-1=t��xn-1��2���ɴ��ܹ�֤��{logt��xn-1��+1}�ǵȱ����У���2����logt��xn-1��+1=��logt2+1��•2n-1����
 ���Ӷ�
���Ӷ� ����Dn+1?Dn��һ��n��N*���������an+1��an���ɴ������t��ȡֵ��Χ��
����Dn+1?Dn��һ��n��N*���������an+1��an���ɴ������t��ȡֵ��Χ����3����
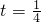 ʱ��
ʱ�� ������
������ ���ɴ��ܹ��ȽϱȽ�Sn��n+7�Ĵ�С��
���ɴ��ܹ��ȽϱȽ�Sn��n+7�Ĵ�С�����������⿼�������벻��ʽ���ۺ����ã�����ʱҪ�������⣬��ϸ���ע���ھ������е����������������ؽ��еȼ�ת����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ