题目内容
已知椭圆![]()
![]()
![]() ,
,
得![]() 且
且![]() 的公共弦
的公共弦![]() 过椭圆
过椭圆![]() 的右焦点。
的右焦点。
⑴当![]() 轴时,求
轴时,求![]() 的值,并判断抛物线
的值,并判断抛物线![]() 的焦点是否在直线
的焦点是否在直线![]() 上;
上;
⑵若![]() ,且抛物线
,且抛物线![]() 的焦点在直线
的焦点在直线![]() 上,求
上,求![]() 的值及直线AB的方程。
的值及直线AB的方程。
(1)m=0,p=9/8, ![]() ,不在直线
,不在直线![]() 上;
上;
(2)![]()
![]()
解析:
⑴当![]() 轴时,点
轴时,点![]()
![]()
从而点![]()
![]()
![]()
此时,![]()
![]() 该焦点不在AB上。
该焦点不在AB上。
⑵当![]() ,由⑴知:
,由⑴知:![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为
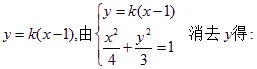
![]() ①
①
设![]() 则
则![]()
因为![]()
![]()
且![]()
从而:![]()
![]()
![]()
![]()
![]() 因为
因为![]() 在直线
在直线![]() 上
上
![]() 即
即![]()
![]()
![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
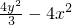 =1有公共的焦点,且椭圆过点P(
=1有公共的焦点,且椭圆过点P( ,1).
,1).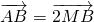 ,求直线l的方程.
,求直线l的方程. +
+ =1的左焦点为F,左准线l与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
=1的左焦点为F,左准线l与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点. =
= ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.