题目内容
已知函数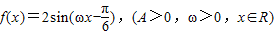 ,且f(x)的最小正周期是2π.
,且f(x)的最小正周期是2π.(1)求ω及f(0)的值;
(2)已知锐角△ABC的三个内角分别为A、B、C,
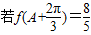 ,
,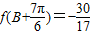 ,求sinC的值.
,求sinC的值.
【答案】分析:(1)根据f(x)的解析式和最小正周期等于2求得ω=1,可得f(x)=2sin(x-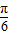 ),从而求得f(0)的值.
),从而求得f(0)的值.
(2)在锐角△ABC中,由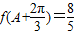 ,求得cosA=
,求得cosA= ,进而得到sinA=
,进而得到sinA= .同理求得sinB=
.同理求得sinB=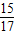 ,cosB=
,cosB=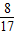 .
.
再利用两角和的正弦公式求得sinC=sin(A+B) 的值.
解答:解:(1)∵函数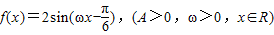 ,且f(x)的最小正周期是2π.
,且f(x)的最小正周期是2π.
∴2π=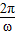 ,ω=1,故f(x)=2sin(x-
,ω=1,故f(x)=2sin(x-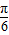 ),∴f(0)=2sin(-
),∴f(0)=2sin(-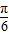 )=-1.
)=-1.
(2)在锐角△ABC中,∵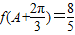 ,∴2sin(A-
,∴2sin(A-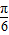 +
+ )=
)= ,∴cosA=
,∴cosA= ,∴sinA=
,∴sinA= .
.
∵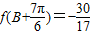 ,∴2sin(B-
,∴2sin(B-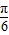 +
+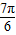 )=-
)=-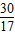 ,∴sinB=
,∴sinB= ,cosB=
,cosB=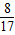 .
.
∴sinC=sin(A+B)=sinAcosB+cosAsinB=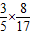 +
+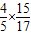 =
=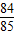 .
.
点评:本题主要考查符合三角函数的对称性,两角和的正弦公式、诱导公式的应用,属于中档题.
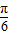 ),从而求得f(0)的值.
),从而求得f(0)的值.(2)在锐角△ABC中,由
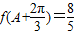 ,求得cosA=
,求得cosA= ,进而得到sinA=
,进而得到sinA= .同理求得sinB=
.同理求得sinB=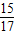 ,cosB=
,cosB=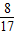 .
.再利用两角和的正弦公式求得sinC=sin(A+B) 的值.
解答:解:(1)∵函数
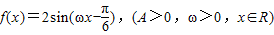 ,且f(x)的最小正周期是2π.
,且f(x)的最小正周期是2π.∴2π=
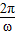 ,ω=1,故f(x)=2sin(x-
,ω=1,故f(x)=2sin(x-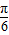 ),∴f(0)=2sin(-
),∴f(0)=2sin(-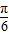 )=-1.
)=-1.(2)在锐角△ABC中,∵
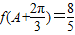 ,∴2sin(A-
,∴2sin(A-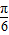 +
+ )=
)= ,∴cosA=
,∴cosA= ,∴sinA=
,∴sinA= .
.∵
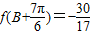 ,∴2sin(B-
,∴2sin(B-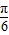 +
+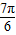 )=-
)=-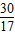 ,∴sinB=
,∴sinB= ,cosB=
,cosB=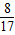 .
.∴sinC=sin(A+B)=sinAcosB+cosAsinB=
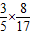 +
+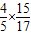 =
=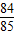 .
.点评:本题主要考查符合三角函数的对称性,两角和的正弦公式、诱导公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
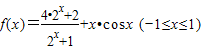 ,且f(x)存在最大值M和最小值N,则M、N一定满足( )
,且f(x)存在最大值M和最小值N,则M、N一定满足( ) ,且f(x)=3,则x= .
,且f(x)=3,则x= . ,且f(x)=3,则x= .
,且f(x)=3,则x= .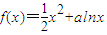 ,且f(x)在区间[1,e](e为自然对数的底数)上的最大值为
,且f(x)在区间[1,e](e为自然对数的底数)上的最大值为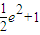 ,求a的值.
,求a的值.