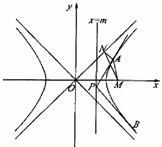
题目内容
点P(x0,y0)在椭圆![]() 1(a>b>0)上,x0=
1(a>b>0)上,x0=![]() , y0=
, y0=![]() . 直线
. 直线![]() 与直线
与直线![]() :
:![]() 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() .
.
(Ⅰ)证明:点P是椭圆![]() 与直线
与直线![]() 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan![]() ,tan
,tan![]() ,tan
,tan![]() 构成等比数列。
构成等比数列。
(I)(方法一)由![]() 得
得![]() 代入椭圆
代入椭圆![]() ,
,
得![]() .
.
将 代入上式,得
代入上式,得![]() 从而
从而![]()
因此,方程组 有唯一解
有唯一解 ,即直线
,即直线![]() 与椭圆有唯一交点P.
与椭圆有唯一交点P. ![]()
(方法二)显然P是椭圆与![]() 的交点,若Q
的交点,若Q![]() 是椭圆与
是椭圆与![]() 的交点,代入
的交点,代入![]() 的方程
的方程![]() ,得
,得![]()
即![]() 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由![]() 可得
可得![]()
椭圆在点P处的切线斜率
切线方程为![]() 即
即![]() 。
。
因此,![]() 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线![]() 的唯一交点。
的唯一交点。
(II)![]()
![]() 的斜率为
的斜率为![]()
![]() 的斜率为
的斜率为![]()
由此得![]()
![]() 构成等比数列。
构成等比数列。
解析:
本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。

练习册系列答案
相关题目