题目内容
设命题p:方程x2-mx+
=0没有实数根.命题q:方程
+
=1表示的曲线是双曲线.若命题p∧q为真命题,求实数m的取值范围.
| 1 |
| 4 |
| x2 |
| m-2 |
| y2 |
| m |
∵方程x2-mx+
=0没有实数根,
则△=m2-1<0?-1<m<1,
∴命题p为真时,-1<m<1;
∵方程
+
=1表示的曲线是双曲线,则(m-2)m<0⇒0<m<2
∴命题q为真时,0<m<2,
若命题p∧q为真命题,
则p真且q真?
?0<m<1,
故m的取值范围是(0,1).
| 1 |
| 4 |
则△=m2-1<0?-1<m<1,
∴命题p为真时,-1<m<1;
∵方程
| x2 |
| m-2 |
| y2 |
| m |
∴命题q为真时,0<m<2,
若命题p∧q为真命题,
则p真且q真?
|
故m的取值范围是(0,1).

练习册系列答案
相关题目
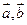 都是非零向量,那么命题“
都是非零向量,那么命题“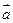 与
与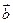 共线”是命题“
共线”是命题“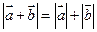 ”的( )
”的( )