题目内容
已知两个非零向量 ,且
,且 与
与 的夹角是钝角或直角,则m+n的取值范围是( )
的夹角是钝角或直角,则m+n的取值范围是( )A.

B.[2,6]
C.

D.(2,6)
【答案】分析:由题意得,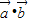 ≤0,(m-2)2+(n-2)2≤2,点(m,n)在以(2,2)为圆心,以
≤0,(m-2)2+(n-2)2≤2,点(m,n)在以(2,2)为圆心,以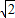 为半径的圆面上,
为半径的圆面上,
包含圆,但不包括直线y=x与圆的2个交点,令m≤2+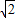 cosθ,n≤2+
cosθ,n≤2+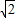 sinθ,则m+n=4+2sin(θ+
sinθ,则m+n=4+2sin(θ+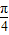 ),
),
由sinθ和cosθ 不能相等或相反,可得-1<sin(θ+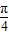 )<1,从而求得m+n 的范围.
)<1,从而求得m+n 的范围.
解答:解:∵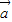 与
与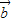 的夹角是钝角或直角,∴
的夹角是钝角或直角,∴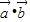 ≤0,∴(m-1)(m-3)+(n-1)(n-3)≤0,
≤0,∴(m-1)(m-3)+(n-1)(n-3)≤0,
即 (m-2)2+(n-2)2≤2,故点(m,n)在以(2,2)为圆心,以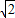 为半径的圆面上,
为半径的圆面上,
包含圆,但不包括直线y=x与圆的2个交点(否则两个向量共线).
可令m≤2+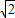 cosθ,n≤2+
cosθ,n≤2+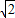 sinθ,则 sinθ和cosθ 不能相等或相反,∴-1<sin(θ+
sinθ,则 sinθ和cosθ 不能相等或相反,∴-1<sin(θ+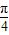 )<1,
)<1,
∴m+n=4+2sin(θ+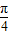 )∈(2,6),
)∈(2,6),
故选D.
点评:本题考查用两个向量的数量积表示两个向量的夹角,正弦函数的值域,得到(m-2)2+(n-2)2≤2,是解题的关键.
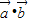 ≤0,(m-2)2+(n-2)2≤2,点(m,n)在以(2,2)为圆心,以
≤0,(m-2)2+(n-2)2≤2,点(m,n)在以(2,2)为圆心,以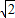 为半径的圆面上,
为半径的圆面上,包含圆,但不包括直线y=x与圆的2个交点,令m≤2+
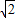 cosθ,n≤2+
cosθ,n≤2+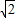 sinθ,则m+n=4+2sin(θ+
sinθ,则m+n=4+2sin(θ+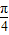 ),
),由sinθ和cosθ 不能相等或相反,可得-1<sin(θ+
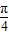 )<1,从而求得m+n 的范围.
)<1,从而求得m+n 的范围.解答:解:∵
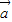 与
与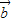 的夹角是钝角或直角,∴
的夹角是钝角或直角,∴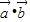 ≤0,∴(m-1)(m-3)+(n-1)(n-3)≤0,
≤0,∴(m-1)(m-3)+(n-1)(n-3)≤0,即 (m-2)2+(n-2)2≤2,故点(m,n)在以(2,2)为圆心,以
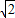 为半径的圆面上,
为半径的圆面上,包含圆,但不包括直线y=x与圆的2个交点(否则两个向量共线).
可令m≤2+
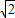 cosθ,n≤2+
cosθ,n≤2+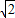 sinθ,则 sinθ和cosθ 不能相等或相反,∴-1<sin(θ+
sinθ,则 sinθ和cosθ 不能相等或相反,∴-1<sin(θ+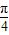 )<1,
)<1,∴m+n=4+2sin(θ+
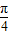 )∈(2,6),
)∈(2,6),故选D.
点评:本题考查用两个向量的数量积表示两个向量的夹角,正弦函数的值域,得到(m-2)2+(n-2)2≤2,是解题的关键.

练习册系列答案
相关题目
 ,且
,且 与
与 的夹角是钝角或直角,则m+n的取值范围是( )
的夹角是钝角或直角,则m+n的取值范围是( )

 ,且
,且 与
与 的夹角是钝角或直角,则m+n的取值范围是( )
的夹角是钝角或直角,则m+n的取值范围是( )

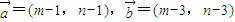 ,且
,且 与
与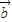 的夹角是钝角或直角,则m+n的取值范围是( )
的夹角是钝角或直角,则m+n的取值范围是( )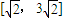

 ,且
,且 与
与 的夹角是钝角或直角,则m+n的取值范围是
的夹角是钝角或直角,则m+n的取值范围是
