题目内容
13.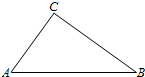 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.(1)求t1与f(t1)的值;
(2)已知警员的对讲机的有效通话距离是3千米.当t1≤t≤1时,求f(t)的表达式,并判断f(t)在[t1,1]上的最大值是否超过3?说明理由.
分析 (1)由题意可得t1=$\frac{AC}{{v}_{乙}}$=$\frac{3}{8}$h,由余弦定理可得f(t1)=PC=$\sqrt{A{C}^{2}+A{P}^{2}-2AC•AP•cosA}$,代值计算可得;
(2)当t1≤t≤$\frac{7}{8}$时,由已知数据和余弦定理可得f(t)=PQ=$\sqrt{25{t}^{2}-42t+18}$,当$\frac{7}{8}$<t≤1时,f(t)=PB=5-5t,综合可得当$\frac{3}{8}$<t≤1时,f(t)∈[0,$\frac{3\sqrt{41}}{8}$],可得结论.
解答 解:(1)由题意可得t1=$\frac{AC}{{v}_{乙}}$=$\frac{3}{8}$h,
设此时甲运动到点P,则AP=v甲t1=5×$\frac{3}{8}$=$\frac{15}{8}$千米,
∴f(t1)=PC=$\sqrt{A{C}^{2}+A{P}^{2}-2AC•AP•cosA}$
=$\sqrt{{3}^{2}+(\frac{15}{8})^{2}-2×3×\frac{15}{8}×\frac{3}{5}}$=$\frac{3\sqrt{41}}{8}$千米;
(2)当t1≤t≤$\frac{7}{8}$时,乙在CB上的Q点,设甲在P点,
∴QB=AC+CB-8t=7-8t,PB=AB-AP=5-5t,
∴f(t)=PQ=$\sqrt{Q{B}^{2}+P{B}^{2}-2QB•PB•cosB}$
=$\sqrt{(7-8t)^{2}+(5-5t)^{2}-2(7-8t)(5-5t)0.8}$
=$\sqrt{25{t}^{2}-42t+18}$,
当$\frac{7}{8}$<t≤1时,乙在B点不动,设此时甲在点P,
∴f(t)=PB=AB-AP=5-5t
∴f(t)=$\left\{\begin{array}{l}{\sqrt{25{t}^{2}-42t+18},\frac{3}{8}≤t≤\frac{7}{8}}\\{5-5t,\frac{7}{8}<t≤1}\end{array}\right.$
∴当$\frac{3}{8}$<t≤1时,f(t)∈[0,$\frac{3\sqrt{41}}{8}$],
故f(t)的最大值没有超过3千米.
点评 本题考查解三角形的实际应用,涉及余弦定理和分段函数,属中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
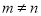 ,两个等差数列
,两个等差数列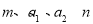 与
与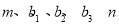 的公差为
的公差为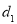 和
和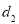 ,则
,则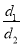 的值为________.
的值为________. 值为___________.
值为___________.