Question

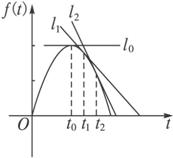
下图表示物体运动的路程随时间变化的函数f(t)=4t-2t²的图象,试根据图象,描述,比较曲线f(t)在t₀,t₁,t₂附近的变化情况,并求出t=2时的切线的方程.

Answer 1

解：用曲线f(t)在t₀,t₁,t₂处的切线刻画曲线f(t)在t₀,t₁,t₂附近的变化情况.

(1)当t=t₀时,曲线f(t)在t₀处的切线l₀平行于x轴.所以在t=t₀附近曲线比较平坦,几乎没有升降.

(2)当t=t₁时,曲线f(t)在t₁处的切线l₁的斜率f′(t₁)＜0,所以在t=t₁附近曲线下降,即函数f(t)在t=t₁附近单调递减.

(3)当t=t₂时,曲线f(t)在t₂处的切线l₂的斜率f′(t₂)＜0,所以在t=t₂附近曲线下降,即函数f(t)在t=t₂附近也单调递减.由图象可以看出,直线l₁的倾斜程度小于直线l₂的倾斜程度,说明曲线f(t)在t₁附近比在t₂附近下降得缓慢.

(4)当t=2时,f(2)=0.

在t=2时的切线的斜率k=f′(2)=?

=

=

= (-2Δt-4)=-4.

所以切线的方程为y=-4(x-2),

即4x+y-8=0.

点评：f(t)对t的导数即为在该点处的切线的斜率，应明确导数的几何意义.