题目内容
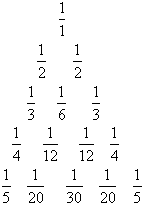 (2012•云南模拟)如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为
(2012•云南模拟)如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为| 1 |
| n |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 360 |
| 1 |
| 360 |
分析:根据“莱布尼兹调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨辉三角形中的每一个数Cnr都换成分数
,就得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,进而可得第10行第3个数.
| 1 | ||
(n+1
|
解答:解:将杨晖三角形中的每一个数Cnr都换成分数
,就得到莱布尼兹三角形.
∵杨晖三角形中第n(n≥3)行第3个数字是Cn-12,
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是
=
,
∴第10行第3个数
=
.
故答案为:
.
| 1 | ||
|
∵杨晖三角形中第n(n≥3)行第3个数字是Cn-12,
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是
| 1 | ||
|
| 2 |
| n×(n-1)×(n-2) |
∴第10行第3个数
| 2 |
| 10×9×8 |
| 1 |
| 360 |
故答案为:
| 1 |
| 360 |
点评:本题考查归纳推理,解题的关键是通过观察分析归纳各数的关系,考查学生的观察分析和归纳能力,属中档题.

练习册系列答案
相关题目
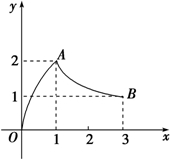 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(