题目内容
下列命题:
(1)在△ABC中,“A<B”是“sinA<sinB”的必要而非充分条件;
(2)函数f(x)=|sinx-cosx|的最小正周期是π;
(3)在△ABC中,若AB=2
,AC=2
,B=
,则△ABC为钝角三角形;
(4)要得到函数y=sin(
-
)的图象,只需将y=sin
的图象向右平移
个单位.
其中真命题的序号是______.
(1)在△ABC中,“A<B”是“sinA<sinB”的必要而非充分条件;
(2)函数f(x)=|sinx-cosx|的最小正周期是π;
(3)在△ABC中,若AB=2
| 2 |
| 3 |
| π |
| 3 |
(4)要得到函数y=sin(
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 4 |
其中真命题的序号是______.
(1)在△ABC中,若A,B均为锐角,由A<B?sinA<sinB.若A为锐角,B为钝角,因为A+B<π,
所以A<π-B<
,所以sinA<sin(π-B)=sinB.反之,在△ABC中,若sinA<sinB,则sinA-sinB<0,
即sin
cos
<0,因为0<A<π,0<B<π,0<A+B<π,所以-
<
<
,0<
<
,
所以cos
>0,则sin
<0,所以A-B<0,即A<B.
所以,在△ABC中,“A<B”是“sinA<sinB”的充要条件.所以,(1)不正确;
(2)由f(x)=|sinx-cosx|=|sin(x-
)|,因为函数y=sin(x-
)的周期为2π,所以,函数f(x)=|sinx-cosx|的最小正周期是π.所以(2)正确;
(3)在△ABC中,由
=
,因为AB=2
,AC=2
,B=
,所以
=
,
解得:sinC=
,由三角形中大边对大角知C=
.所以A=π-(
+
)=
.
所以△ABC为锐角三角形.所以(3)不正确;
(4)函数y=sin(
-
)=sin
(x-
),所以,要得到函数y=sin(
-
)的图象,只需将y=sin
的图象向右平移
个单位.所以,(4)不正确.
故真命题的序号是(2).
故答案为(2).
所以A<π-B<
| π |
| 2 |
即sin
| A-B |
| 2 |
| A+B |
| 2 |
| π |
| 2 |
| A-B |
| 2 |
| π |
| 2 |
| A+B |
| 2 |
| π |
| 2 |
所以cos
| A+B |
| 2 |
| A-B |
| 2 |
所以,在△ABC中,“A<B”是“sinA<sinB”的充要条件.所以,(1)不正确;
(2)由f(x)=|sinx-cosx|=|sin(x-
| π |
| 4 |
| π |
| 4 |
(3)在△ABC中,由
| AC |
| sinB |
| AB |
| sinC |
| 2 |
| 3 |
| π |
| 3 |
2
| ||
sin
|
2
| ||
| sinC |
解得:sinC=
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| 5π |
| 12 |
所以△ABC为锐角三角形.所以(3)不正确;
(4)函数y=sin(
| x |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| x |
| 2 |
| π |
| 2 |
故真命题的序号是(2).
故答案为(2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
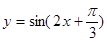 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; 的图象和函数
的图象和函数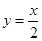 的图象有三个公共点;
的图象有三个公共点;