题目内容
 已知函数y=Asin(ωx+φ)(x∈R,A>0,ω,0,|φ|<
已知函数y=Asin(ωx+φ)(x∈R,A>0,ω,0,|φ|<| π | 2 |
(1)求f(x)的解析式;
(2)求f(x)最小正周期以及使f(x)取最小值的x的集合;
(3)求f(x)的单调递增区间和递减区间.
分析:(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数的解析式.
(2)由f(x)最小正周期为
,运算求得结果,要使f(x)取最小值,需sin(
x+
)=-1,故
x+
=2kπ-
,k∈z,由此求得使f(x)取最小值的x的集合.
(3)令2kπ-
≤(
x+
)≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.令2kπ+
≤(
x+
)≤2kπ+
,k∈z,求得x的范围,可得函数的减区间.
(2)由f(x)最小正周期为
| 2π |
| ω |
| 2 |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
(3)令2kπ-
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
解答:解:(1)由函数y=Asin(ωx+φ)(x∈R,A>0,ω,0,|φ|<
)的图象可得A=2,由
•T=
•
=
-
=
,∴ω=
.
再由五点法作图可得
×
+φ=
,∴φ=
,故函数y=2sin(
x+
).
(2)由(1)可得f(x)最小正周期为
=
=3π.
要使f(x)取最小值,有sin(
x+
)=-1,故
x+
=2kπ-
,k∈z,解得 x=3kπ-
,
故使f(x)取最小值的x的集合为 {x|x=3kπ-
,k∈z}.
(3)令2kπ-
≤(
x+
)≤2kπ+
,k∈z,可得3kπ-
≤x≤3kπ+
,故函数的增区间为[3kπ-
,3kπ+
],k∈z.
令2kπ+
≤(
x+
)≤2kπ+
,k∈z,可得3kπ+
≤x≤3kπ+
,故函数的增区间为[3kπ+
,3kπ+
],k∈z.
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| 7π |
| 4 |
| π |
| 4 |
| 3π |
| 2 |
| 2 |
| 3 |
再由五点法作图可得
| 2 |
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
(2)由(1)可得f(x)最小正周期为
| 2π |
| ω |
| 2π | ||
|
要使f(x)取最小值,有sin(
| 2 |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 4 |
故使f(x)取最小值的x的集合为 {x|x=3kπ-
| 5π |
| 4 |
(3)令2kπ-
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
令2kπ+
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 4 |
| 7π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的周期性与求法,求得函数y=Asin(ωx+∅)的单调区间与最值,属于中档题.

练习册系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
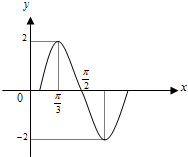 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数