题目内容
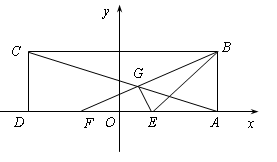
在矩形 中,以
中,以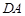 所在直线为
所在直线为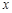 轴,以
轴,以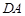 中点
中点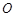 为坐标原点,建立如图所示的平面直角坐标系.已知点
为坐标原点,建立如图所示的平面直角坐标系.已知点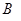 的坐标为
的坐标为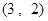 ,E、F为
,E、F为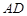 的两个三等分点,
的两个三等分点,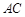 和
和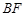 交于点
交于点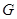 ,
,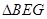 的外接圆为⊙
的外接圆为⊙ .
.
(1)求证: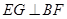 ;
;
(2)求⊙ 的方程;
的方程;
(3)设点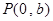 ,过点P作直线与⊙
,过点P作直线与⊙ 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数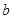 的取值范围.
的取值范围.
 中,以
中,以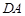 所在直线为
所在直线为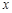 轴,以
轴,以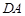 中点
中点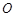 为坐标原点,建立如图所示的平面直角坐标系.已知点
为坐标原点,建立如图所示的平面直角坐标系.已知点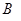 的坐标为
的坐标为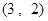 ,E、F为
,E、F为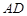 的两个三等分点,
的两个三等分点,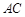 和
和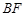 交于点
交于点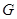 ,
,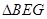 的外接圆为⊙
的外接圆为⊙ .
. 
(1)求证:
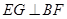 ;
;(2)求⊙
 的方程;
的方程;(3)设点
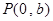 ,过点P作直线与⊙
,过点P作直线与⊙ 交于M,N两点,若点M恰好是线段PN的中点,求实数
交于M,N两点,若点M恰好是线段PN的中点,求实数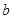 的取值范围.
的取值范围.(1)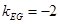 ,
,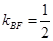 ,根据
,根据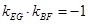 。
。
(2)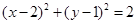 .
.
(3)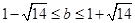 .
.
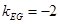 ,
,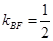 ,根据
,根据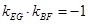 。
。(2)
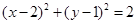 .
. (3)
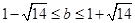 .
.试题分析:(1)由题意可知
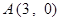 ,
,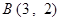 ,
,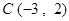 ,
,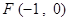 .
.所以直线
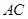 和直线
和直线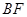 的方程分别为:
的方程分别为: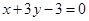 ,
,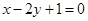 ,
,由
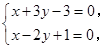 解得
解得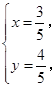 所以
所以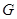 点的坐标为
点的坐标为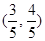 . 6分
. 6分所以
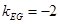 ,
,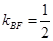 ,
,因为
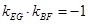 ,所以
,所以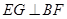 , 8分
, 8分(2)由(1)知⊙
 的圆心为
的圆心为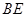 中点
中点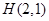 ,半径为
,半径为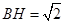 ,
,所以⊙
 方程为
方程为 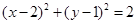 . 10分
. 10分(3) 设
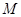 点的坐标为
点的坐标为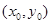 ,则
,则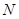 点的坐标为
点的坐标为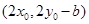 ,
,因为点
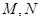 均在⊙
均在⊙ 上,所以
上,所以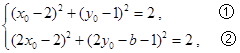 ,
,由②-①×4,得
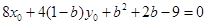 ,
,所以点
 在直线
在直线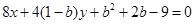 , 12分
, 12分又因为点
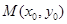 在⊙
在⊙ 上,
上,所以圆心
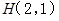 到直线
到直线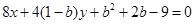 的距离
的距离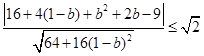
 , 14分
, 14分即
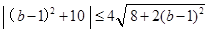 ,
,整理,得
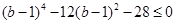 ,即
,即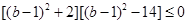 ,
,所以
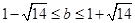 ,故
,故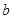 的取值范围为
的取值范围为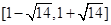 . 16分
. 16分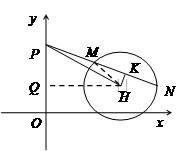
解法二:过
 作
作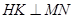 交
交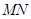 于
于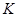 ,
,设
 到直线
到直线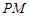 的距离
的距离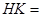
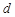 ,则
,则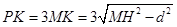 ,
,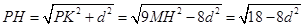 ,
,又因为
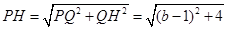
所以
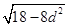
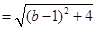 ,
,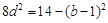 ,因为
,因为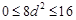 ,
,所以
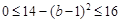 ,所以
,所以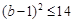 ,
,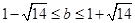 ;
;解法三:因为
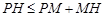 ,
,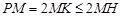 ,所以
,所以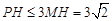
所以
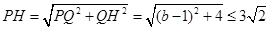 ,所以
,所以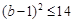 ,
,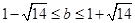 .
.点评:中档题,直线方程的考查中,点斜式是一重点考查内容。两直线垂直的条件是,斜率乘积为-1,或一条直线斜率为0,另一直线的斜率不存在。直线与圆的位置关系问题,往往利用“几何法”更为直观、简单。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 的弦AB的中点,则直线AB的方程为( )
的弦AB的中点,则直线AB的方程为( )



 与
与 平行,则
平行,则 的值为( )
的值为( )


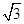 x+1的倾斜角的
x+1的倾斜角的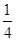 ,且分别满足下列条件的直线方程:
,且分别满足下列条件的直线方程: 与直线
与直线 平行,则实数
平行,则实数 的值为 .
的值为 . 的倾斜角为
的倾斜角为 的直线
的直线 与圆
与圆 交于
交于 两点,则
两点,则 .
.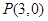 作直线
作直线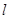 ,使它被两相交直线
,使它被两相交直线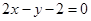 和
和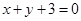 所截得的线段
所截得的线段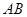 恰好被
恰好被 点平分,求直线
点平分,求直线