题目内容
19．已知函数f（x）=ln（4-x2），则f（x）的定义域为（-2，2），当x=0时，f（x）有最大值ln4．分析 根据真数大于0，求出函数的定义域，再根据函数的性质求出函数的最大值点和最大值．
解答 解：由4-x2＞0得：x∈（-2，2），
即函数f（x）的定义域为（-2，2）；
当x=0时，4-x2取最大值4，
函数f（x）=ln（4-x2）取最大值ln4，
故答案为：（-2，2），0，ln4；
点评 本题考查了函数的定义域的定义域，函数的最值，熟练掌握对数函数的图象和性质是解答的关键．
练习册系列答案
相关题目
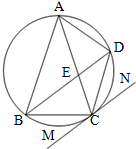如图，四边形ABCD内接于圆，AB=AC，直线MN切圆于点C，BD∥MN交AC于点E．若AB=6，BC=4，则AE的长为$\frac{10}{3}$．
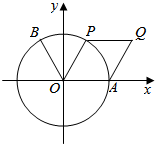如图，点B（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），点A时单位圆与x轴正半轴的交点．设点P为单位圆上的动点，点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$，∠AOP=2θ（$\frac{π}{6}$≤θ＜$\frac{π}{2}$），f（θ）=$\overrightarrow{OB}$•$\overrightarrow{OQ}$，求f（θ）的取值范围，当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时，求四边形OAQP的面积．