题目内容
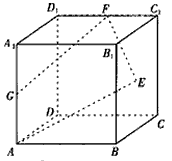
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F、G分别是棱C1D1,AA1的中点。设点E1,G1分别是点E,G在平面DCC1D1内的正投影,
(1)求以E为顶点,以四边形FGAE在平面DCC1D1内的正投影为底面边界的棱锥的体积;
(2)证明:直线FG1⊥平面FEE1;
(3)求异面直线E1G1与EA所成角的正弦值。
(1)求以E为顶点,以四边形FGAE在平面DCC1D1内的正投影为底面边界的棱锥的体积;
(2)证明:直线FG1⊥平面FEE1;
(3)求异面直线E1G1与EA所成角的正弦值。
解:(1)依题作点E、G在平面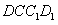 内的正投影
内的正投影 ,
,
则 分别为
分别为 的中点,
的中点,
连接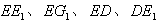 ,
,
则所求为四棱锥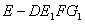 的体积,
的体积,
其底面 面积为
面积为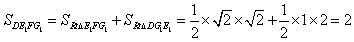 ,
,
又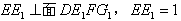 ,
,
∴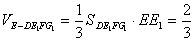 。
。
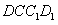 内的正投影
内的正投影 ,
,则
 分别为
分别为 的中点,
的中点,连接
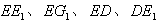 ,
,则所求为四棱锥
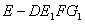 的体积,
的体积,其底面
 面积为
面积为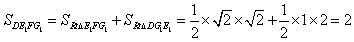 ,
,又
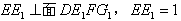 ,
,∴
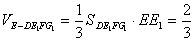 。
。(2)以D为坐标原点,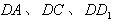 所在直线分别作x轴,y轴,z轴,
所在直线分别作x轴,y轴,z轴,
得 ,
,
又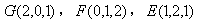 ,
,
则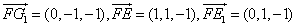 ,
,
∴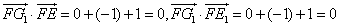 ,
,
即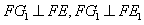 ,
,
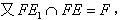
∴ 。
。
(3)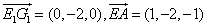 ,
,
则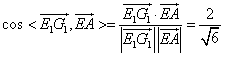 ,
,
设异面直线E1G1与EA所成角为θ,
则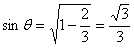 。
。
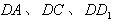 所在直线分别作x轴,y轴,z轴,
所在直线分别作x轴,y轴,z轴,得
 ,
,又
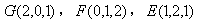 ,
,则
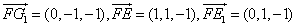 ,
,∴
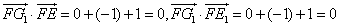 ,
,即
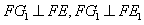 ,
,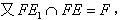
∴
 。
。(3)
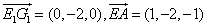 ,
,则
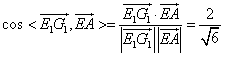 ,
,设异面直线E1G1与EA所成角为θ,
则
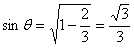 。
。 
练习册系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )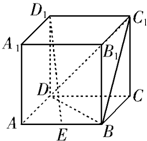 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.