题目内容
已知 .
.(1)求证:
 与
与 互相垂直;
互相垂直;(2)若
 与
与 大小相等(其中k为非零实数),求β-α.
大小相等(其中k为非零实数),求β-α.
【答案】分析:(1)由条件求出 与
与 的坐标,计算
的坐标,计算 的值等于零,从而证得结论.
的值等于零,从而证得结论.
(2)先求出 与
与 的解析式,由
的解析式,由 得2kcos(β-α)=-2kcos(β-α),求得cos(β-α)=0从而得到β-α的值.
得2kcos(β-α)=-2kcos(β-α),求得cos(β-α)=0从而得到β-α的值.
解答:解:(1)由 ,
,
得 ,
, ,
,
又 =cos2α-cos2β+sin2α-sin2β=0.
=cos2α-cos2β+sin2α-sin2β=0.
∴ .
.
(2)∵ ,
,
∴ ,
,
同理∴ ,
,
由 得2kcos(β-α)=-2kcos(β-α),
得2kcos(β-α)=-2kcos(β-α),
又k≠0,所以cos(β-α)=0,因0<α<β<π,所以 .
.
点评:本题主要考查两个向量数量积公式的应用,两个向量垂直的条件,求向量的模的方法,属于中档题.
 与
与 的坐标,计算
的坐标,计算 的值等于零,从而证得结论.
的值等于零,从而证得结论.(2)先求出
 与
与 的解析式,由
的解析式,由 得2kcos(β-α)=-2kcos(β-α),求得cos(β-α)=0从而得到β-α的值.
得2kcos(β-α)=-2kcos(β-α),求得cos(β-α)=0从而得到β-α的值.解答:解:(1)由
 ,
,得
 ,
, ,
,又
 =cos2α-cos2β+sin2α-sin2β=0.
=cos2α-cos2β+sin2α-sin2β=0.∴
 .
.(2)∵
 ,
,∴
 ,
,同理∴
 ,
,由
 得2kcos(β-α)=-2kcos(β-α),
得2kcos(β-α)=-2kcos(β-α),又k≠0,所以cos(β-α)=0,因0<α<β<π,所以
 .
.点评:本题主要考查两个向量数量积公式的应用,两个向量垂直的条件,求向量的模的方法,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 .
. 与
与 互相垂直;
互相垂直;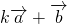 与
与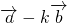 大小相等(其中k为非零实数),求β-α.
大小相等(其中k为非零实数),求β-α.
 的三条侧棱
的三条侧棱 、
、 、
、 两两垂直,且长度均为2.
两两垂直,且长度均为2. 、
、 分别是
分别是 、
、 的中点,
的中点, 是
是 的中点,过
的中点,过 、
、 、
、 ,已知
,已知 .
. ⊥面
⊥面 ;
; 的大小.
的大小.
 .
. 与
与 互相垂直;
互相垂直; 与
与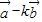 大小相等(其中k为非零实数),求β-α.
大小相等(其中k为非零实数),求β-α.