题目内容
(本小题满分12分)
如图,在直三棱柱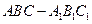 中,
中,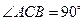 ,
,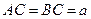 ,
,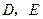 分别为棱
分别为棱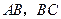 的中点,
的中点,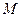 为棱
为棱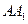 上的点,二面角
上的点,二面角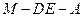 为
为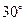 .
.
(I)证明: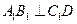 ;
;
(II)求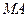 的长,并求点
的长,并求点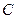 到平面
到平面 的距离.
的距离.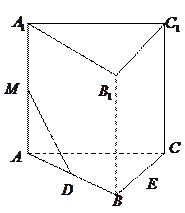
如图,在直三棱柱
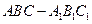 中,
中,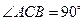 ,
,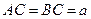 ,
,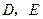 分别为棱
分别为棱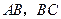 的中点,
的中点,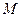 为棱
为棱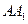 上的点,二面角
上的点,二面角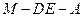 为
为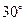 .
.(I)证明:
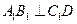 ;
;(II)求
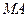 的长,并求点
的长,并求点 到平面
到平面 的距离.
的距离.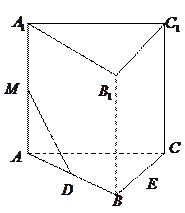
(I)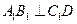
(II)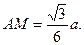 C到平面MDE的距离与A到平面MDE的距离相等,为
C到平面MDE的距离与A到平面MDE的距离相等,为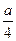
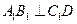
(II)
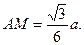 C到平面MDE的距离与A到平面MDE的距离相等,为
C到平面MDE的距离与A到平面MDE的距离相等,为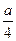
)证明:连结CD.
∵三棱柱ABC-A,BC是直三棱柱.
∴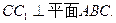
∴CD为C1D在平面ABC内的射影.
∵△ABC中,AC=BC,D为AB中点.
∴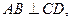
∴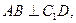
∵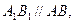
∴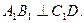
(Ⅱ)解法一:过点A作CE的平行线,交ED的延长线于F,连结MF.
∵D、E分别为AB、BC的中点.
∵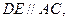
又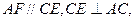
∴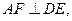
∵AF为MF在平面ABC内的射影,
∴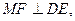
∴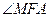 为二面角
为二面角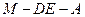 的平面角,
的平面角,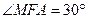 .
.
在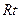 △MAF中,
△MAF中,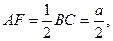
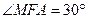 ,
,
∴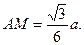
作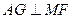 ,垂足为G.
,垂足为G.
∵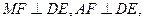
∴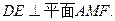
∴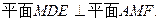
∴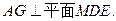
在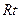 △GAF中,
△GAF中,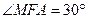 ,AF=
,AF=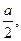
∴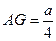 ,即A到平面MDE的距离为
,即A到平面MDE的距离为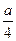 .
.
∵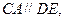 ∴
∴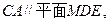
∴C到平面MDE的距离与A到平面MDE的距离相等,为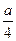 ,
,
解法二:过点A作CE的平行线,交ED的延长线于F,连结MF.
∵D、E分别为AB、CB的中点,
∴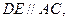
又∵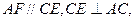
∴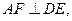
∵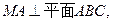
∴AF为MF在平面ABC内的射影,
∴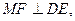
∴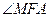 为二面角
为二面角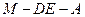 的平面角,
的平面角,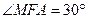 .
.
在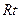 △MAF中,
△MAF中,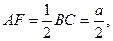
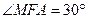 ,
,
∴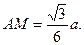
设C到平面MDE的距离为h.
∵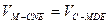 ,
,
∴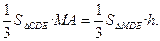
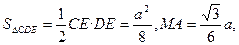
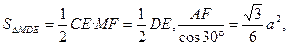
∴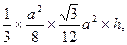
∴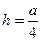 ,即C到平面MDE的距离相等,为
,即C到平面MDE的距离相等,为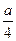
∵三棱柱ABC-A,BC是直三棱柱.
∴
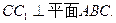
∴CD为C1D在平面ABC内的射影.
∵△ABC中,AC=BC,D为AB中点.
∴
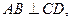
∴
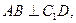
∵
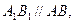
∴
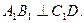
(Ⅱ)解法一:过点A作CE的平行线,交ED的延长线于F,连结MF.
∵D、E分别为AB、BC的中点.
∵
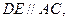
又
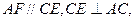
∴
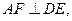
∵AF为MF在平面ABC内的射影,
∴
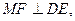
∴
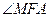 为二面角
为二面角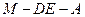 的平面角,
的平面角,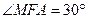 .
.在
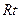 △MAF中,
△MAF中,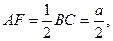
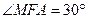 ,
,∴
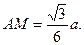
作
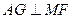 ,垂足为G.
,垂足为G.∵
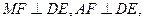
∴
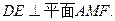
∴
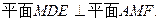
∴
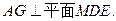
在
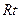 △GAF中,
△GAF中,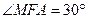 ,AF=
,AF=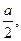
∴
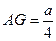 ,即A到平面MDE的距离为
,即A到平面MDE的距离为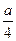 .
.∵
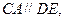 ∴
∴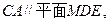
∴C到平面MDE的距离与A到平面MDE的距离相等,为
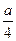 ,
,解法二:过点A作CE的平行线,交ED的延长线于F,连结MF.
∵D、E分别为AB、CB的中点,
∴
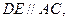
又∵
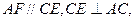
∴
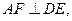
∵
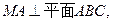
∴AF为MF在平面ABC内的射影,
∴
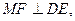
∴
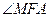 为二面角
为二面角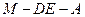 的平面角,
的平面角,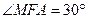 .
.在
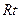 △MAF中,
△MAF中,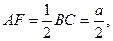
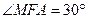 ,
,∴
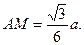
设C到平面MDE的距离为h.
∵
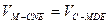 ,
,∴
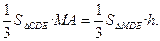
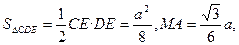
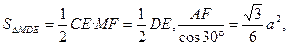
∴
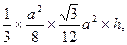
∴
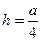 ,即C到平面MDE的距离相等,为
,即C到平面MDE的距离相等,为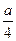

练习册系列答案
相关题目
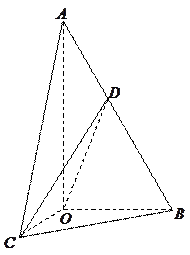
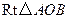 中,
中,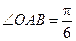 ,斜边
,斜边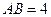 .
.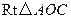 可以通过
可以通过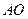 为轴旋转得到,且二面角
为轴旋转得到,且二面角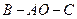 是直二面角.动点
是直二面角.动点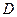 的斜边
的斜边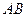 上.
上.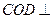 平面
平面 ;
;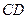 所成角的大小;
所成角的大小;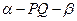 ,
,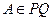 ,
,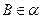 ,
,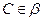 ,
,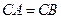 ,
,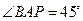 ,直线
,直线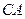 和平面
和平面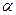 所成的角为
所成的角为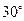 .
.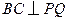 ;
;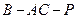 的大小.
的大小.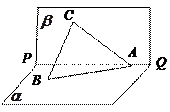
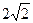 .
. (2)在线段
(2)在线段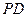 上是否存在一点
上是否存在一点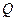 ,使
,使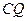 与平面
与平面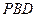 所成的角的正弦值为
所成的角的正弦值为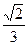 ,若存在,
,若存在, ,直线
,直线 ,给出下列命题:
,给出下列命题: ∥
∥ ; ②
; ② ∥m;
∥m; ∥
∥ ; ④
; ④ ∥
∥
 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则
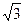 ,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.
,⊙O为其内切圆,D为BC的中点,将三角形ACD沿AD折叠,使二面角B-AD-C成直二面角,则⊙O上的圆弧扫过的曲面面积为____________.