题目内容
符号[x]表示不超过x的最大整数，如：[π]=3，[-1.5]=-2，定义函数f（x）=x-[x]，那么下列命题中正确的个数是（ ）
①函数f（x）的定义域为R，值域为[0，1]
②方程f（x）=
有无数解
③函数f（x）是周期函数
④函数f（x）是R上的增函数．
①函数f（x）的定义域为R，值域为[0，1]
②方程f（x）=
| 1 |
| 2 |
③函数f（x）是周期函数
④函数f（x）是R上的增函数．
分析：根据新定义的函数f（x）=x-[x]，可以画出其图象根据图象就比较容易判断了；
解答：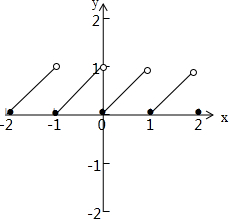
解：∵符号[x]表示不超过x的最大整数，如：[π]=3，[-1.5]=-2，定义函数f（x）=x-[x]，
∴当x为整数时，f（x）=0，
∴函数f（x）的图象如下：
可以看出f（x）的定义域为R，值域为[0，1），故①错误；
方程f（x）=
有无数解是正确的，故②正确，
由图象f（x）是以周期为1的函数，但不是在定义域R上的增函数，故③正确，④错误；
故选B．
解：∵符号[x]表示不超过x的最大整数，如：[π]=3，[-1.5]=-2，定义函数f（x）=x-[x]，∴当x为整数时，f（x）=0，
∴函数f（x）的图象如下：
可以看出f（x）的定义域为R，值域为[0，1），故①错误；
方程f（x）=
| 1 |
| 2 |
由图象f（x）是以周期为1的函数，但不是在定义域R上的增函数，故③正确，④错误；
故选B．
点评：此题考查新定义，根据新定义画出f（x）=）=x-[x]，的图象则此题就很简单了，关于符号[x]表示不超过x的最大整数，同学们要知道．
练习册系列答案
相关题目