题目内容
在△ABC中，∠BAC=
，
=1，
=2，点E，F是边BC的三等分点，则
•
．
| π |
| 3 |
| |AB| |
| |AC| |
| AE |
| AF |
分析：先判定三角形形状，然后建立直角坐标系，分别求出向量
、
的坐标，代入向量数量积的运算公式，即可求出答案．
| AE |
| AF |
解答：解：∵在△ABC中，∠BAC=
，
=1，
=2，
由余弦定理可知BC=
=
∵三边满足勾股定理，∴∠CBA=90°
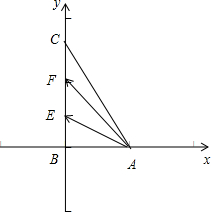
以B为坐标原点，BA、BC方向为x，y轴正方向建立坐标系，
可得B（0，0），A（1，0），C（0，
）
又∵E，F分别是Rt△ABC中BC上的两个三等分点，
则E（0，
），F（0，
），
则
=（-1，
），
=（-1，
）
∴
•
=1+
=
，
故答案为：
| π |
| 3 |
| |AB| |
| |AC| |
由余弦定理可知BC=
12+22-2×1×2×
|
| 3 |
∵三边满足勾股定理，∴∠CBA=90°
以B为坐标原点，BA、BC方向为x，y轴正方向建立坐标系，
可得B（0，0），A（1，0），C（0，
| 3 |
又∵E，F分别是Rt△ABC中BC上的两个三等分点，
则E（0，
| ||
| 3 |
2
| ||
| 3 |
则
| AE |
| ||
| 3 |
| AF |
2
| ||
| 3 |
∴
| AE |
| AF |
| 2 |
| 3 |
| 5 |
| 3 |
故答案为：
| 5 |
| 3 |
点评：本题考查平面向量数量积的运算，将向量数量积的运算坐标化是解决问题的关键，属中档题．
练习册系列答案
相关题目
如图，在△ABC中，在△ABC中
等于（ ）
| a+b |
| a-b |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|