题目内容
短轴长为8，离心率为
的椭圆两焦点分别为F1、F2，过点F1作直线l交椭圆于A、B两点，则△ABF2的周长为
| 3 | 5 |
20
20
．分析：确定椭圆的长轴长，利用椭圆的定义，可得△ABF2的周长．
解答：解：∵椭圆的短轴长为8，离心率为
，
∴2b=8，
=
∴a=5，b=4，c=3
∵过点F1作直线l交椭圆于A、B两点，
∴△ABF2的周长为4a=20
故答案为：20
| 3 |
| 5 |
∴2b=8，
| c |
| a |
| 3 |
| 5 |
∴a=5，b=4，c=3
∵过点F1作直线l交椭圆于A、B两点，
∴△ABF2的周长为4a=20
故答案为：20
点评：本题考查椭圆的几何性质，考查椭圆定义的运用，属于基础题．
练习册系列答案
相关题目
，那么椭圆的标准方程为
或
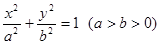的焦点F1，F2，短轴长为8，离心率为
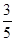，过F1的直线交椭圆于A、B两点，则
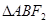的周长为（ ）
的椭圆两焦点分别为F1、F2，过点F1作直线l交椭圆于A、B两点，则△ABF2的周长为________．
的焦点F1，F2，短轴长为8，离心率为
，过F1的直线交椭圆于A、B两点，则
的周长为（ ）